Paljud koolilapsed unustavad keskkooli jõudes ära pika jagamise. Arvutid, kalkulaatorid, Mobiiltelefonid ja muud seadmed on meie ellu nii tihedalt sisenenud, et elementaarsed matemaatilised tehted viivad mõnikord stuuporini. Ja kuidas inimesed ilma kõigi nende hüvedeta paarkümmend aastat tagasi hakkama said? Esiteks peate meeles pidama peamised jagamiseks vajalikud matemaatilised mõisted. Niisiis, dividend on arv, mis jagatakse. Jagaja – arv, millega jagatakse. Tulemusena saadud tulemusi nimetatakse jagatiseks. Ribaks jagamiseks kasutage kooloniga sarnast sümbolit - ":" ja veeruks jagamisel ikooni "∟"; seda nimetatakse ka nurgaks.
Samuti tasub meeles pidada, et iga jagamist saab kontrollida korrutamisega. Jagamise tulemuse kontrollimiseks korrutage see lihtsalt jagajaga; tulemuseks peaks olema arv, mis vastab dividendile (a: b=c; seega c*b=a). Nüüd sellest, mis on kümnendmurd. Kümnendmurd saadakse, jagades ühiku arvuga 0,0, 1000 jne. Nende arvude salvestamine ja nendega tehtavad matemaatilised tehted on täpselt samad, mis täisarvude puhul. Kümnendmurdude jagamisel ei pea meeles pidama, kus nimetaja asub. Kõik selgub numbri üleskirjutamisel. Kõigepealt kirjutatakse täisarv, ja pärast koma kirjutatakse selle kümnendik, sajandik, tuhandik. Esimene number pärast koma vastab kümnetele, teine sadadele, kolmas tuhandetele jne.
Iga õpilane peaks teadma, kuidas kümnendmurde jagada kümnend. Kui nii dividend kui ka jagaja korrutada sama number, siis vastus, st jagatis ei muutu. Kui kümnendmurd korrutada 0,0, 1000 jne, siis täisarvu järel olev koma muudab oma asukohta – see liigub paremale sama arvu numbrite võrra, kui palju on korrutatud arvus nulle. Näiteks kümnendkoha korrutamisel 10-ga liigub koma ühe numbri võrra paremale. 2,9: 6,7 – korrutame nii jagaja kui ka dividendi 100-ga, saame 6,9: 3687. Kõige parem on korrutada nii, et sellega korrutades ei jääks vähemalt ühele arvule (jagajale või dividendile) pärast koma ühtegi numbrit. , st tehke vähemalt üks arv täisarvuks. Veel mõned näited täisarvu järel komade liigutamisest: 9,2: 1,5 = 2492: 2,5; 5,4:4,8 = 5344:74598.
Tähelepanu, kümnendmurd ei muuda oma väärtust, kui paremale küljele lisatakse nullid, näiteks 3,8 = 3,0. Samuti ei muutu murru väärtus, kui nullid numbri lõpust eemaldatakse paremalt: 3,0 = 3,3. Nulle aga numbri keskelt eemaldada ei saa – 3,3. Kuidas jagada kümnendkohaga naturaalarv veerus? Kümnendmurru jagamiseks naturaalarvuga veerus tuleb teha vastav märge nurgaga, jagada. Jagatis tuleb täisarvu jagamise lõppedes panna koma. Näiteks 5,4|2 14 7,2 18 18 0 4 4 0Kui dividendinumbri esimene number on jagajast väiksem, kasutatakse järgnevaid numbreid, kuni on võimalik sooritada esimene tegevus.
IN sel juhul, dividendi esimene number on 1, seda ei saa jagada 2-ga, seega kasutame jagamisel korraga kahte numbrit 1 ja 5: 15 jagatakse 2-ga ülejäänud osaga, see osutub jagatiseks 7 ja jääk jääb 1. Seejärel kasutame dividendi järgmist numbrit - 8. Liigume alla 1-ni ja jagame 18 2-ga. Jagatisesse kirjutame arvu 9. Ülejäägisse ei jää midagi, seega kirjutame 0. nihutage ülejäänud dividendi number 4 allapoole ja jagage jagajaga, st 2-ga. Jagatisesse kirjutame 2 ja jääk on jälle 0. Selle jagamise tulemuseks on arv 7,2. Seda nimetatakse privaatseks. Kümnendkoha kümnendkohaga jagamise küsimust on üsna lihtne lahendada, kui tead mõnda nippi. Kümnendkohtade mõtteline jagamine on mõnikord üsna keeruline, seetõttu kasutatakse protsessi hõlbustamiseks pikka jagamist.
Selle jagamise korral kehtivad samad reeglid, mis kümnendmurdu täisarvuga jagamisel või stringiks jagamisel. Rea vasakule küljele kirjutavad nad dividendi, seejärel panevad sümboli "nurk" ja seejärel jagaja ning alustavad jagamist. Jagamise hõlbustamiseks ja täisarvu järel oleva koma sobivasse kohta viimiseks võite korrutada kümnete, sadade või tuhandetega. Näiteks 9,2: 1,5 = 24920: 125. Tähelepanu, mõlemad murrud korrutatakse 0,0 1000-ga. Kui dividend korrutati 10-ga, siis korrutatakse ka jagaja 10-ga. B selles näites nii dividend kui ka jagaja korrutati 100-ga. Järgmisena tehakse arvutus samamoodi, nagu on näidatud kümnendmurru naturaalarvuga jagamise näites. 0,1-ga jagamiseks; 0,1; 0,1 jne on vaja nii jagaja kui ka dividend korrutada 0,0, 1000-ga.
Üsna sageli saadakse jagatisega jagamisel, st vastuses, lõpmatuid murde. Sel juhul on vaja arv ümardada kümnendikku, sajandikku või tuhandikku. Sel juhul kehtib reegel: kui pärast arvu, milleni vastus tuleb ümardada, on väiksem või võrdne 5-ga, siis vastus ümardatakse alla, aga kui see on suurem kui 5, siis ümardatakse üles. Näiteks soovite tulemuse 5,5 ümardada tuhandikuteks. See tähendab, et vastus pärast koma peaks lõppema numbriga 6. Pärast 6 on 9, mis tähendab, et ümardame vastuse üles ja saame 5,7. Aga kui vastust 5.5 oleks vaja ümardada mitte tuhandikuteks, vaid kümnenditeks, siis näeks vastus välja selline - 5.2. Sel juhul ei ümardatud 2 üles, kuna sellele järgneb 3 ja see on väiksem kui 5.
Koolis uuritakse neid toiminguid lihtsatest kuni keerukateni. Seetõttu on hädavajalik mõista põhjalikult nende toimingute sooritamise algoritmi lihtsaid näiteid. Nii et hiljem ei tekiks raskusi kümnendmurdude veergu jagamisega. Lõppude lõpuks on see selliste ülesannete kõige raskem versioon.
See teema nõuab järjepidevat õppimist. Lünkad teadmistes on siin vastuvõetamatud. Iga õpilane peaks selle põhimõtte selgeks õppima juba esimeses klassis. Seega, kui jätate mitu õppetundi järjest vahele, peate materjali iseseisvalt omandama. Muidu ei teki hiljem probleeme mitte ainult matemaatikaga, vaid ka teiste sellega seotud ainetega.
Teiseks nõutav tingimus Edukas matemaatika õppimine – liikuge pika jagamise näidete juurde alles pärast liitmise, lahutamise ja korrutamise omandamist.
Lapsel on raske jagada, kui ta pole korrutustabelit õppinud. Muide, seda on parem õpetada Pythagorase tabeli abil. Midagi üleliigset pole ja korrutamist on sel juhul lihtsam õppida.
Kuidas korrutatakse naturaalarvud veerus?
Kui jagamise ja korrutamise veerus olevate näidete lahendamisel tekib raskusi, peaksite hakkama probleemi lahendama korrutamisega. Kuna jagamine on korrutamise pöördtehing:
- Enne kahe arvu korrutamist peate neid hoolikalt vaatama. Valige see, millel on rohkem numbreid (pikem) ja kirjutage see kõigepealt üles. Asetage teine selle alla. Pealegi peavad vastava kategooria numbrid olema sama kategooria all. See tähendab, et esimese numbri parempoolseim number peaks olema teise numbri parempoolseimast numbrist kõrgemal.
- Korrutage alumise numbri parempoolseim number ülemise numbri iga numbriga, alustades paremalt. Kirjutage vastus rea alla nii, et selle viimane number oleks selle numbri all, millega korrutasite.
- Korrake sama teise väiksema numbri numbriga. Kuid korrutamise tulemust tuleb nihutada ühe numbri võrra vasakule. Sel juhul jääb selle viimane number alla selle numbri, millega see korrutati.
Jätkake seda korrutamist veerus, kuni teise teguri arvud saavad otsa. Nüüd tuleb need kokku voltida. See on vastus, mida otsite.

Algoritm kümnendkohtade korrutamiseks
Esiteks peate ette kujutama, et antud murrud ei ole kümnendkohad, vaid loomulikud. See tähendab, et eemaldage neilt komad ja seejärel jätkake eelmises juhtumis kirjeldatud viisil.
Erinevus algab siis, kui vastus on kirja pandud. Sel hetkel on vaja kokku lugeda kõik arvud, mis ilmuvad mõlemas murdes pärast koma. Just nii palju tuleb neid vastuse lõpust kokku lugeda ja sinna koma panna.
Seda algoritmi on mugav illustreerida näitega: 0,25 x 0,33:

Kust alustada jaotuse õppimist?
Enne pikkade jagamise näidete lahendamist peate meeles pidama pika jagamise näites esinevate numbrite nimesid. Esimene neist (see, mis on jagatud) on jagatav. Teine (jagatuna) on jagaja. Vastus on privaatne.
Pärast seda, kasutades lihtsat igapäevast näidet, selgitame selle matemaatilise tehte olemust. Näiteks kui võtate 10 maiustust, on neid lihtne ema ja isa vahel võrdselt jagada. Aga mis siis, kui peate need oma vanematele ja vennale kinkima?
Pärast seda saate tutvuda jagamisreeglitega ja need selgeks õppida konkreetsed näited. Kõigepealt lihtsad ja seejärel liikuge järjest keerulisemate juurde.
Algoritm arvude jagamiseks veergu

Esiteks esitame ühekohalise arvuga jaguvate naturaalarvude protseduuri. Need on ka mitmekohaliste jagajate või kümnendmurdude aluseks. Alles siis peaksite tegema väikseid muudatusi, kuid sellest hiljem:
- Enne pika jagamise tegemist peate välja selgitama, kus on dividend ja jagaja.
- Kirjutage dividend üles. Sellest paremal on jaotur.
- Joonistage nurk vasakule ja alla viimase nurga lähedale.
- Määrake mittetäielik dividend, st arv, mis on jagamisel minimaalne. Tavaliselt koosneb see ühest numbrist, maksimaalselt kahest.
- Vali number, mis vastuses esimesena kirjutatakse. See peaks olema arv, mitu korda jagaja dividendi mahub.
- Kirjutage selle arvu jagajaga korrutamise tulemus.
- Kirjutage see mittetäieliku dividendi alla. Tehke lahutamine.
- Lisage jäägile esimene number pärast juba jagatud osa.
- Valige vastuseks uuesti number.
- Korrake korrutamist ja lahutamist. Kui ülejäänud võrdne nulliga ja dividend on läbi, siis on näide tehtud. Vastasel juhul korrake samme: eemaldage arv, võtke arv üles, korrutage, lahutage.
Kuidas lahendada pikka jagamist, kui jagajas on rohkem kui üks number?
Algoritm ise langeb täielikult kokku ülalkirjeldatuga. Erinevus on mittetäieliku dividendi numbrite arv. Nüüd peaks neid olema vähemalt kaks, kuid kui need osutuvad jagajast väiksemaks, peate töötama kolme esimese numbriga.
Selles jaotuses on veel üks nüanss. Fakt on see, et jääk ja sellele lisatud arv ei ole mõnikord jagajaga jagatavad. Seejärel tuleb järjekorras lisada veel üks number. Aga vastus peab olema null. Kui jagamine viiakse läbi kolmekohalised numbrid veerus, peate võib-olla eemaldama rohkem kui kaks numbrit. Seejärel kehtestatakse reegel: vastuses peaks olema üks null vähem kui eemaldatud numbrite arv.
Seda jaotust saate kaaluda näite abil - 12082: 863.
- Selles mittetäielikuks dividendiks osutub number 1208. Arv 863 on sellesse paigutatud vaid korra. Seetõttu peaks vastus olema 1 ja 1208 alla kirjutage 863.
- Pärast lahutamist on jääk 345.
- Peate sellele lisama numbri 2.
- Arv 3452 sisaldab 863 neli korda.
- Vastuseks tuleb kirja panna neli. Pealegi, kui korrutada 4-ga, on see täpselt saadud arv.
- Ülejäänud osa pärast lahutamist on null. See tähendab, et jaotus on lõpetatud.
Vastus näites oleks number 14.
Mis siis, kui dividend lõpeb nulliga?
Või paar nulli? Sel juhul on jääk null, kuid dividend sisaldab ikkagi nulle. Pole vaja heita meelt, kõik on lihtsam, kui võib tunduda. Piisab, kui lisada vastusele lihtsalt kõik jagamata jäänud nullid.
Näiteks tuleb 400 jagada 5-ga. Mittetäielik dividend on 40. Viis mahub sinna 8 korda. See tähendab, et vastuseks tuleks kirjutada 8. Lahutamisel ei jää üle jääki. See tähendab, et jagunemine on lõpetatud, kuid dividendi jääb null. See tuleb vastusele lisada. Seega 400 jagamine 5-ga võrdub 80-ga.

Mida teha, kui on vaja kümnendmurdu jagada?
Jällegi näeb see arv välja naturaalarvuna, kui mitte koma, mis eraldab kogu osa murdosast. See viitab sellele, et kümnendmurdude jagamine veergu on sarnane ülalkirjeldatule.
Ainus erinevus on semikoolon. See tuleks lisada vastusesse kohe, kui murdosa esimene number on eemaldatud. Teine võimalus seda öelda on järgmine: kui olete kogu osa jagamise lõpetanud, pange koma ja jätkake lahendamist.
Kümnendmurdudega pika jagamise näidete lahendamisel tuleb meeles pidada, et komajärgsele osale saab lisada suvalise arvu nulle. Mõnikord on see vajalik numbrite täitmiseks.

Kahe kümnendkoha jagamine
See võib tunduda keeruline. Aga ainult alguses. Lõppude lõpuks on juba selge, kuidas jagada murdude veergu naturaalarvuga. See tähendab, et peame selle näite taandada juba tuttavaks vormiks.
Seda on lihtne teha. Peate mõlemad murdarvud korrutama 10, 100, 1000 või 10 000-ga ja võib-olla ka miljoniga, kui probleem seda nõuab. Kordaja peaks olema valitud selle järgi, mitu nulli on jagaja kümnendosas. See tähendab, et tulemuseks on see, et peate murdosa jagama naturaalarvuga.
Ja see on halvim stsenaarium. Võib ju juhtuda, et selle toimingu dividendist saab täisarv. Seejärel taandatakse näite lahendus fraktsioonide veerguks jagamisega väga suureks lihtne variant: tehted naturaalarvudega.
Näiteks jagage 28,4 3,2-ga:
- Esmalt tuleb need korrutada 10-ga, kuna teisel arvul on pärast koma ainult üks koht. Korrutamine annab 284 ja 32.
- Nad peaksid olema eraldatud. Lisaks on täisarv 284 korda 32.
- Esimene vastuseks valitud number on 8. Korrutades saadakse 256. Ülejäänud arv on 28.
- Kogu osa jagamine on lõppenud ja vastuses on vaja koma.
- Eemaldage jäägiks 0.
- Võtke uuesti 8.
- Ülejäänud: 24. Lisage sellele veel 0.
- Nüüd peate võtma 7.
- Korrutamise tulemus on 224, jääk on 16.
- Võtke maha veel 0. Võtke igaüks 5 ja saate täpselt 160. Ülejäänud osa on 0.
Jaotus on lõpetatud. Näite 28,4:3,2 tulemus on 8,875.
Mis siis, kui jagaja on 10, 100, 0,1 või 0,01?

Nii nagu korrutamise puhul, pole ka siin pikka jagamist vaja. Piisab lihtsalt koma liigutamisest teatud arvu numbrite jaoks soovitud suunas. Lisaks saate seda põhimõtet kasutades lahendada näiteid nii täisarvude kui ka kümnendmurdudega.
Seega, kui peate jagama 10, 100 või 1000-ga, nihutatakse koma vasakule sama arvu numbrite võrra, kui jagajas on nullid. See tähendab, et kui arv jagub 100-ga, peab koma kahe numbri võrra vasakule liikuma. Kui dividend on naturaalarv, siis eeldatakse, et koma on lõpus.
See toiming annab sama tulemuse, nagu oleks see arv korrutatud 0,1, 0,01 või 0,001-ga. Nendes näidetes nihutatakse koma ka murdosa pikkusega võrdse arvu numbrite võrra vasakule.
Jagades 0,1-ga (jne) või korrutades 10-ga (jne), peaks koma nihkuma ühe koha võrra paremale (või kahe, kolme võrra, olenevalt nullide arvust või murdosa pikkusest).
Tasub teada, et dividendis antud numbrite arv ei pruugi olla piisav. Seejärel saab puuduvad nullid lisada vasakule (terves osas) või paremale (pärast koma).

Perioodiliste murdude jagamine
Sel juhul ei ole veergu jagamisel võimalik täpset vastust saada. Kuidas lahendada näidet, kui kohtate punktiga murdosa? Siin peame liikuma tavaliste murdude juurde. Ja seejärel jagage need eelnevalt õpitud reeglite järgi.
Näiteks peate 0.(3) jagama 0,6-ga. Esimene murdosa on perioodiline. See teisendab murdarvuks 3/9, mis vähendades annab 1/3. Teine murd on viimane koma. Seda on veelgi lihtsam üles kirjutada nagu tavaliselt: 6/10, mis võrdub 3/5. Harilike murdude jagamise reegel nõuab jagamise asendamist korrutisega ja jagaja pöördarvuga. See tähendab, et näide taandub 1/3 korrutamisele 5/3-ga. Vastus on 5/9.
Kui näide sisaldab erinevaid murde...
Siis on võimalikud mitmed lahendused. Esiteks, harilik murd Võite proovida selle kümnendkohaks teisendada. Seejärel jagage ülaltoodud algoritmi abil kaks kümnendkohta.
Teiseks saab iga viimase kümnendmurru kirjutada hariliku murruna. Kuid see pole alati mugav. Enamasti osutuvad sellised murded tohututeks. Ja vastused on tülikad. Seetõttu peetakse esimest lähenemisviisi eelistatavamaks.
Vaatame selles valguses näiteid kümnendkohtade jagamisest.
Näide.
Jagage kümnendmurd 1,2 kümnendmurruga 0,48.
Lahendus.
Vastus:
1,2:0,48=2,5 .
Näide.
Jagage perioodiline kümnendmurd 0.(504) kümnendmurruga 0,56.
Lahendus.
Teisendame perioodilise kümnendmurru tavaliseks murruks: . Teisendame ka viimase kümnendmurru 0,56 tavaliseks murruks, meil on 0,56 = 56/100. Nüüd saame liikuda algsete kümnendkohtade jagamiselt harilike murdude jagamisele ja lõpetada arvutused: .
Teisendame saadud hariliku murru kümnendmurruks, jagades lugeja veeruga nimetajaga:
Vastus:
0,(504):0,56=0,(900) .
Lõpmatute mitteperioodiliste kümnendmurdude jagamise põhimõte erineb lõplike ja perioodiliste kümnendmurdude jagamise põhimõttest, kuna mitteperioodilisi kümnendmurde ei saa teisendada tavalisteks murdudeks. Lõpmatute mitteperioodiliste kümnendmurdude jagamine taandatakse lõplike kümnendmurdude jagamiseks, mille jaoks teostame numbrite ümardamine kuni teatud tasemeni. Veelgi enam, kui üks arvudest, millega jagamine toimub, on lõplik või perioodiline kümnendmurd, ümardatakse see ka sama numbrini kui mitteperioodiline kümnendmurd.
Näide.
Jagage lõpmatu mitteperioodiline koma 0,779... lõpliku kümnendkoha arvuga 1,5602.
Lahendus.
Kõigepealt peate ümardama kümnendkohad, et saaksite liikuda lõpmatute mitteperioodiliste kümnendkohtade jagamiselt lõplike kümnendkohtade jagamisele. Saame ümardada lähima sajandikuni: 0,779…≈0,78 ja 1,5602≈1,56. Seega 0,779…:1,5602≈0,78:1,56= 78/100:156/100=78/100·100/156= 78/156=1/2=0,5 .
Vastus:
0,779…:1,5602≈0,5 .
Naturaalarvu jagamine kümnendmurruga ja vastupidi
Naturaalarvu kümnendmurruga jagamise ja kümnendmurdu naturaalarvuga jagamise lähenemisviisi olemus ei erine kümnendmurdude jagamise olemusest. See tähendab, et lõplikud ja perioodilised murrud asendatakse tavaliste murdudega ning lõpmatud mitteperioodilised murrud ümardatakse.
Illustreerimiseks vaadake näidet kümnendmurru jagamisest naturaalarvuga.
Näide.
Jagage kümnendmurd 25,5 naturaalarvuga 45.
Lahendus.
Asendades kümnendmurru 25,5 hariliku murruga 255/10=51/2, taandatakse jagamine hariliku murru jagamisele naturaalarvuga:. Saadud murdarvu kümnendmärgistuses on vorm 0,5(6) .
Vastus:
25,5:45=0,5(6) .
Kümnendmurru jagamine naturaalarvuga veeruga
Lõplikud kümnendmurrud on mugav jagada naturaalarvudeks veeruga analoogselt naturaalarvude veeruga jagamisega. Toome välja jagamise reegli.
To jagage kümnendmurd naturaalarvuga, kasutades veergu, vajalik:
- lisage jagatavast kümnendmurdust paremale mitu numbrit 0 (jagamise käigus saate vajadusel lisada suvalise arvu nulle, kuid neid nulle ei pruugi vaja minna);
- jagage kümnendmurru veeruga naturaalarvuga vastavalt kõigile naturaalarvude veeruga jagamise reeglitele, kuid kui kümnendmurru kogu osa jagamine on lõpetatud, peate jagatisesse panema koma ja jätkake jagamist.
Ütleme kohe, et lõpliku kümnendmurru naturaalarvuga jagamise tulemusena saad kas lõpliku kümnendmurru või lõpmatu perioodilise kümnendmurru. Tõepoolest, pärast kõigi mitte-0 komakohtade jagamise lõpetamist jagatav murd, jääk võib olla 0 ja me saame lõpliku kümnendmurru või hakkavad jäägid perioodiliselt korduma ja saame perioodilise kümnendmurru.
Mõistame näidete lahendamisel veerus kümnendmurdude naturaalarvudega jagamise kõiki nõtkusi.
Näide.
Jagage kümnendmurd 65,14 4-ga.
Lahendus.
Jagame kümnendmurru veeru abil naturaalarvuga. Lisame murru 65,14 tähistuses paremale paar nulli ja saame võrdse kümnendmurru 65,1400 (vt võrdsed ja ebavõrdsed kümnendmurrud). Nüüd saate hakata jagama veeruga kümnendmurru 65.1400 täisarvu naturaalarvuga 4: 
See lõpetab kümnendmurru täisarvu jagamise. Siin jagatis peate panema koma ja jätkama jagamist: 
Oleme jõudnud jäägini 0, selles etapis veeruga jagamine lõpeb. Selle tulemusena on meil 65,14:4=16,285.
Vastus:
65,14:4=16,285 .
Näide.
Jagage 164,5 27-ga.
Lahendus.
Jagame kümnendmurru veeru abil naturaalarvuga. Pärast kogu osa jagamist saame järgmise pildi: 
Nüüd paneme jagatisesse koma ja jätkame veeruga jagamist: 
Nüüd on selgelt näha, et jäägid 25, 7 ja 16 on hakanud korduma, samas kui jagatis korduvad numbrid 9, 2 ja 5. Seega, jagades kümnendkoha 164,5 27-ga, saame perioodilise kümnendkoha 6,0(925) .
Vastus:
164,5:27=6,0(925) .
Kümnendmurdude veergude jagamine
Kümnendmurru jagamist kümnendmurruga saab taandada kümnendmurru jagamisele naturaalarvuga veeruga. Selleks tuleb dividend ja jagaja korrutada sellise arvuga nagu 10 või 100 või 1000 jne, nii et jagajast saab naturaalarv ning seejärel jagada naturaalarvuga veeruga. Seda saame teha tänu jagamise ja korrutamise omadustele, kuna a:b=(a·10):(b·10) , a:b=(a·100):(b·100) jne.
Teisisõnu, lõpu kümnendkoha jagamiseks lõpu kümnendkohaga, vaja:
- dividendis ja jagajas liigutage koma paremale nii mitme koha võrra, kui palju on jagajas pärast koma; kui dividendis pole koma liigutamiseks piisavalt märke, peate lisama vajaliku arvu koma nullid paremale;
- Pärast seda jagage kümnendveeruga naturaalarvuga.
Näite lahendamisel kaaluge selle kümnendmurruga jagamise reegli rakendamist.
Näide.
Jagage veeruga 7,287 2,1-ga.
Lahendus.
Liigutame koma nendes kümnendmurdudes ühe numbri võrra paremale, see võimaldab liikuda kümnendmurru 7.287 jagamiselt kümnendmurruga 2.1 kümnendmurru 72.87 jagamisele naturaalarvuga 21. Jagame veergude järgi: 
Vastus:
7,287:2,1=3,47 .
Näide.
Jagage koma 16,3 kümnendkohaga 0,021.
Lahendus.
Liigutage dividendi ja jagaja koma kolme paremasse kohta. Ilmselgelt ei ole jagajal koma liigutamiseks piisavalt numbreid, seega lisame paremale vajaliku arvu nulle. Nüüd jagame veeruga murdosa 16300,0 naturaalarvuga 21: 
Sellest hetkest hakkavad jäägid 4, 19, 1, 10, 16 ja 13 korduma, mis tähendab, et korduvad ka jagatis olevad numbrid 1, 9, 0, 4, 7 ja 6. Selle tulemusena saame perioodilise kümnendmurru 776,(190476) .
Vastus:
16,3:0,021=776,(190476) .
Pange tähele, et väljakuulutatud reegel võimaldab teil jagada naturaalarvu veeruga viimaseks kümnendmurruks.
Näide.
Jagage naturaalarv 3 kümnendmurruga 5.4.
Lahendus.
Pärast koma ühe koha võrra paremale nihutamist jõuame arvu 30,0 jagamiseni 54-ga. Jagame veergude järgi:  .
.
Seda reeglit saab rakendada ka lõpmatu kümnendmurdu jagamisel 10, 100, .... Näiteks 3,(56):1000=0,003(56) ja 593,374…:100=5,93374….
Kümnendkohtade jagamine 0,1, 0,01, 0,001 jne.
Kuna 0,1 = 1/10, 0,01 = 1/100 jne, siis hariliku murruga jagamise reeglist järeldub, et kümnendmurd jagatakse 0,1, 0,01, 0,001 jne. see on sama, mis antud kümnendkoha korrutamine arvuga 10, 100, 1000 jne. vastavalt.
Teisisõnu, kümnendmurru jagamiseks arvudega 0,1, 0,01, ... peate nihutama koma 1, 2, 3, ... numbri võrra paremale ja kui kümnendmurru numbritest ei piisa koma liigutamiseks, siis tuleb õigetele nullidele lisada vajalik arv.
Näiteks 5,739:0,1=57,39 ja 0,21:0,00001=21 000.
Sama reeglit saab rakendada ka lõpmatute kümnendmurdude jagamisel arvudega 0,1, 0,01, 0,001 jne. Sel juhul peaksite perioodiliste murdude jagamisel olema väga ettevaatlik, et mitte eksida jagamise tulemusel saadud murru perioodiga. Näiteks 7.5(716):0.01=757,(167), kuna peale koma liigutamist kümnendmurrus 7.5716716716... kaks kohta paremale on meil kirje 757.167167.... Lõpmatu arvu mitteperioodiliste kümnendmurdudega on kõik lihtsam: 394,38283…:0,001=394382,83… .
Murru või segaarvu jagamine kümnendkohaga ja vastupidi
Hariliku murru või segaarvu jagamine lõpliku või perioodilise kümnendmurruga, samuti lõpliku või perioodilise kümnendmurru jagamine hariliku murru või segaarvuga taandub harilike murdude jagamisele. Selleks asendatakse kümnendmurrud vastavate tavaliste murrudega ja segaarv esitatakse valemurruna.
Lõpmatu mitteperioodilise kümnendmurru jagamisel hariliku murru või segaarvuga ja vastupidi peaksite jätkama kümnendmurdude jagamisega, asendades hariliku murru või segaarvu vastava kümnendmurruga.
Bibliograafia.
- Matemaatika: õpik 5. klassi jaoks. Üldharidus institutsioonid / N. Ya. Vilenkin, V. I. Zhokhov, A. S. Chesnokov, S. I. Shvartsburd. - 21. väljaanne, kustutatud. - M.: Mnemosyne, 2007. - 280 lk.: ill. ISBN 5-346-00699-0.
- Matemaatika. 6. klass: hariv. üldhariduse jaoks institutsioonid / [N. Ya. Vilenkin ja teised]. - 22. väljaanne, rev. - M.: Mnemosyne, 2008. - 288 lk.: ill. ISBN 978-5-346-00897-2.
- Algebra:õpik 8. klassi jaoks. Üldharidus institutsioonid / [Yu. N. Makarychev, N. G. Mindjuk, K. I. Neshkov, S. B. Suvorova]; toimetanud S. A. Teljakovski. - 16. väljaanne. - M.: Haridus, 2008. - 271 lk. : haige. - ISBN 978-5-09-019243-9.
- Gusev V. A., Mordkovich A. G. Matemaatika (juhend tehnikutesse astujatele): Proc. abiraha.- M.; Kõrgem kool, 1984.-351 lk, ill.
Kümnendkohtade lisamine on sama, mis täisarvude liitmine. Vaatame seda näidetega.
1) 0,132 + 2,354. Märgistame terminid üksteise alla.
Siin saadi 2 tuhandiku liitmisel 4 tuhandikule 6 tuhandikku;
3 sajandiku liitmisel 5 sajandikuga on tulemuseks 8 sajandikku;
1 kümnendiku liitmisest 3 kümnendikuga -4 kümnendikku ja
0 täisarvu lisamisest 2 täisarvuga - 2 täisarvu.
2) 5,065 + 7,83.
Teises terminis pole tuhandeid, seega on oluline terminite üksteise järel märgistamisel mitte vigu teha.
3) 1,2357 + 0,469 + 2,08 + 3,90701.
Siin on tuhandikute liitmisel tulemuseks 21 tuhandikku; kirjutasime tuhandete alla 1 ja sajandikutele lisasime 2, nii et sajandikukohas saime järgmised terminid: 2 + 3 + 6 + 8 + 0; kokku annavad 19 sajandikku, meie kirjutasime alla 9 sajandikku ja 1 arvestati kümnendikku jne.
Seega tuleb kümnendmurdude lisamisel järgida järgmist järjekorda: märgi murrud üksteise alla nii, et kõikides terminites paikneksid üksteise all samad numbrid ja kõik komad ühes vertikaalses veerus; Mõne termini kümnendkohtadest paremale lisatakse vähemalt mõttes selline arv nulle, et kõik pärast koma olevad liikmed oleksid ühepalju numbritega. Seejärel lisage numbrite järgi, alustades parem pool, ja saadud summas asetatakse koma samasse vertikaalsesse veergu, kus see nendes terminites asub.
§ 108. Kümnendmurdude lahutamine.
Kümnendkohtade lahutamine toimib samamoodi nagu täisarvude lahutamine. Näitame seda näidetega.
1) 9,87 - 7,32. Märgistame minuendi all oleva alajaotuse nii, et sama numbri ühikud oleksid üksteise all:
2) 16,29 - 4,75. Märgime minuendi all oleva alajaotuse, nagu esimeses näites:
Kümnendike lahutamiseks tuli 6-st võtta üks terve ühik ja jagada see kümnendikku.
3) 14,0213-5,350712. Kirjutame alla minuendi all olevale alajaotusele:
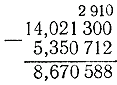
Lahutamine toimus järgmiselt: kuna me ei saa 0-st lahutada 2 miljondikut, siis peaksime pöörama vasakul asuva lähima numbri ehk sajatuhandikesse, kuid sajatuhandiku asemel on ka null, seega võtame 1 kümnetuhandiku. 3 kümnetuhandik ja Me jagame selle sajatuhandikeks, saame 10 sajatuhandikku, millest jätame sajatuhandikesse kategooriasse 9 sajatuhandik ja jagame 1 sajatuhandiku miljoniteks, saame 10 miljondiku. Seega on meil kolmes viimases numbris: miljondik 10, sajatuhandik 9, kümnetuhandik 2. Suurema selguse ja mugavuse huvides (et mitte unustada) on need arvud kirjutatud minuendi vastavate murdarvude kohale. Nüüd saate hakata lahutama. 10 miljondikust lahutame 2 miljondikut, saame 8 miljonit; 9 sajatuhandikest lahutame 1 sajatuhandiku, saame 8 sajatuhandiku jne.
Seega järgitakse kümnendmurdude lahutamisel järgmist järjekorda: märkige minuendi all oleva alajaotuse alla nii, et samad numbrid paikneksid üksteise all ja kõik komad oleksid samas vertikaalses veerus; paremale lisavad nad vähemalt mõttes nii palju nulle minuendis või alamjaotises, et neil oleks sama arv numbreid, seejärel lahutavad nad numbrite kaupa, alustades paremalt poolt ja saadud vahesse panevad koma sama vertikaalne veerg, milles see asub minuendis ja lahutades.
§ 109. Kümnendmurdude korrutamine.
Vaatame mõningaid näiteid kümnendmurdude korrutamisest.
Nende arvude korrutise leidmiseks saame arutleda järgmiselt: kui tegurit suurendada 10 korda, siis on mõlemad tegurid täisarvud ja saame need siis korrutada vastavalt täisarvude korrutamise reeglitele. Kuid me teame, et kui üks teguritest suureneb mitu korda, suureneb toode sama palju. See tähendab, et arv, mis saadakse täisarvuliste tegurite korrutamisel, s.o 28 23-ga, on 10 korda suurem tegelikust korrutisest ja tõelise korrutise saamiseks tuleb leitud korrutist 10 korda vähendada. Seetõttu peate siin üks kord korrutama 10-ga ja üks kord jagama 10-ga, kuid 10-ga korrutamine ja jagamine toimub koma ühe koha võrra paremale ja vasakule nihutades. Seetõttu peate tegema seda: teguris liigutage koma õigesse kohta, see võrdub 23-ga, seejärel peate saadud täisarvud korrutama:
See toode on tegelikust 10 korda suurem. Seetõttu tuleb seda vähendada 10 korda, mille jaoks nihutame koma ühe koha võrra vasakule. Seega saame
28 2,3 = 64,4.
Kontrollimise eesmärgil saab kirjutada kümnendmurru nimetajaga ja sooritada toimingu harilike murdude korrutamise reegli järgi, s.t.
2) 12,27 0,021.
Selle näite erinevus eelmisest seisneb selles, et siin on mõlemad tegurid esitatud kümnendmurdudena. Kuid siin ei pööra me korrutamise käigus tähelepanu komadele, s.t suurendame ajutiselt kordajat 100 korda ja kordajat 1000 korda, mis suurendab korrutist 100 000 korda. Seega, korrutades 1227 21-ga, saame:
1 227 21 = 25 767.
Arvestades, et saadud toode on tegelikust tootest 100 000 korda suurem, peame seda nüüd 100 000 korda vähendama, pannes sellesse õigesti koma, siis saame:
32,27 0,021 = 0,25767.
Kontrollime:
Seega piisab kahe kümnendmurru korrutamiseks komadele tähelepanu pööramata, kui korrutada need täisarvudena ja korrutis eraldada paremal pool komaga nii palju kümnendkohti, kui oli korrutis ja korrutis. kordajas kokku.
Viimase näite tulemuseks oli viie kümnendkohaga korrutis. Kui nii suurt täpsust ei nõuta, ümardatakse kümnendmurd. Ümardamisel peaksite kasutama sama reeglit, mis oli näidatud täisarvude puhul.
§ 110. Korrutamine tabelite abil.
Mõnikord saab kümnendkohtade korrutamist teha tabelite abil. Selleks saab kasutada näiteks neid kahekohaliste arvude korrutustabeleid, mille kirjeldus on antud varem.
1) Korrutage 53 1,5-ga.
Korrutame 53 15-ga. Tabelis on see toode 795. Leidsime toote 53 15-ga, kuid meie teine tegur oli 10 korda väiksem, mis tähendab, et toodet tuleb vähendada 10 korda, st.
53 1,5 = 79,5.
2) Korrutage 5,3 4,7-ga.
Esiteks leiame tabelist korrutise 53 korda 47, see saab olema 2 491. Aga kuna suurendasime kordajat ja kordajat kokku 100 korda, on saadud korrutis 100 korda suurem, kui see peaks olema; seega peame seda toodet 100 korda vähendama:
5,3 4,7 = 24,91.
3) Korrutage 0,53 7,4-ga.
Esiteks leiame tabelist korrutise 53 korda 74; see on 3 922. Aga kuna suurendasime kordajat 100 korda ja kordajat 10 korda, suurenes korrutis 1000 korda; seega peame nüüd seda 1000 korda vähendama:
0,53 7,4 = 3,922.
§ 111. Kümnendmurdude jagamine.
Vaatame kümnendmurdude jagamist järgmises järjekorras:
1. Kümnendmurru jagamine täisarvuga,
1. Jaga kümnendmurd täisarvuga.
1) Jaga 2,46 2-ga.
Jagasime 2-ga kõigepealt terve, siis kümnendiku ja lõpuks sajandikuga.
2) Jaga 32,46 3-ga.
32,46: 3 = 10,82.
Jagasime 3 kümnendikku 3-ga, seejärel hakkasime jagama 2 ühikut 3-ga; kuna dividendi (2) ühikute arv on jagajast (3) väiksem, pidime jagatisesse panema 0; edasi, jäägile võtsime 4 kümnendikku ja jagasime 24 kümnendikku 3-ga; sai jagatis 8 kümnendikku ja jagas lõpuks 6 sajandikku.
3) Jagage 1,2345 5-ga.
1,2345: 5 = 0,2469.
Siin on jagatis esikohal null täisarvu, kuna üks täisarv ei jagu 5-ga.
4) Jaga 13,58 4-ga.

Selle näite eripära on see, et kui saime jagatis 9 sajandikku, avastasime jäägi, mis on võrdne 2 sajandikuga, jagasime selle jäägi tuhandeteks, saime 20 tuhandiku ja lõpetasime jagamise.
Reegel. Kümnendmurru jagamine täisarvuga toimub samamoodi nagu täisarvude jagamine ja saadud jäägid teisendatakse järjest väiksemateks kümnendmurdudeks; Jagamine jätkub, kuni jääk on null.
2. Jaga koma kümnendkohaga.
1) Jaga 2,46 0,2-ga.
Me juba teame, kuidas jagada kümnendmurdu täisarvuga. Mõelgem, kas seda uut jagunemisjuhtumit on võimalik taandada eelmisele? Omal ajal pidasime jagatise märkimisväärseks omaduseks, et see jääb muutumatuks, kui dividend ja jagaja samaaegselt suurenevad või vähenevad sama arv kordi. Kui jagaja oleks täisarv, saaksime meile antud numbreid hõlpsasti jagada. Selleks piisab selle 10-kordsest suurendamisest ja õige jagatise saamiseks on vaja dividendi suurendada sama palju, s.o 10 korda. Seejärel asendatakse nende numbrite jaotus järgmiste numbrite jagamisega:
Lisaks ei ole enam vaja andmetes muudatusi teha.
Teeme selle jaotuse:
Seega 2,46: 0,2 = 12,3.
2) Jaga 1,25 1,6-ga.

Suurendame jagajat (1,6) 10 korda; et jagatis ei muutuks, suurendame dividendi 10 korda; 12 täisarvu ei jagu 16-ga, seega kirjutame jagatisesse 0 ja jagame 125 kümnendikku 16-ga, jagatis saame 7 kümnendikku ja jääk 13. Jagame 13 kümnendikku sajandikuteks, määrates nulli ja jagame 130, sajandikku 16-ga jne. Pange tähele järgmist:
a) kui konkreetses ei ole täisarve, siis kirjutatakse nende asemele null täisarvu;
b) kui pärast dividendi numbri lisamist jäägile saadakse arv, mis jagajaga ei jagu, siis jagatisesse kirjutatakse null;
c) kui pärast dividendi viimase numbri eemaldamist jagamine ei lõpe, siis jagamine jätkub, lisades jäägile nullid;
d) kui dividend on täisarv, siis kümnendmurruga jagamisel suurendatakse seda, lisades sellele nullid.
Seega, arvu kümnendmurruga jagamiseks peate jagaja koma ära jätma ja seejärel suurendama dividendi nii mitu korda, kui palju jagaja selles koma ära jättes suurenes, ning seejärel jagama vastavalt reeglile. kümnendmurru jagamiseks täisarvuga.
§ 112. Ligikaudsed jagatised.
Eelmises lõigus vaatlesime kümnendmurdude jagamist ja kõigis lahendatud näidetes oli jagamine lõpetatud, st saadi täpne jagatis. Enamasti pole aga täpset jagatist võimalik saada, ükskõik kui kaugele jagamist jätkame. Siin on üks selline juhtum: jagage 53 101-ga.

Oleme jagatis juba viis numbrit saanud, kuid jagamine pole veel lõppenud ja pole lootustki, et see kunagi lõppeks, kuna ülejäänus hakkavad meil olema numbrid, mida on juba varem kohatud. Jagatis korduvad ka arvud: on ilmne, et pärast arvu 7 ilmub lõputult arv 5, seejärel 2 jne. Sellistel juhtudel jagamine katkeb ja piirdub jagatise paari esimese numbriga. Seda jagatist nimetatakse lähedased. Näitame näidetega, kuidas jagada jagamist.
Olgu vaja jagada 25 3-ga. Ilmselgelt ei saa sellisest jagamisest täpset jagatist, väljendatuna täis- või kümnendmurruna. Seetõttu otsime ligikaudset jagatist:
25: 3 = 8 ja ülejäänud 1
Ligikaudne jagatis on 8; see on muidugi väiksem kui täpne jagatis, sest seal on jääk 1. Täpse jagatise saamiseks tuleb leitud ligikaudsele jagatisele lisada murd, mis saadakse 1-ga võrdse jäägi jagamisel 3-ga, s.t. , kuni 8; see on murdosa 1/3. See tähendab, et täpne jagatis väljendatakse segaarvuna 8 1/3. Kuna 1/3 on õige murd, st murd, vähem kui üks, siis lubame selle ära visata viga, mis vähem kui üks. Jagatis 8 saab olema ligikaudne jagatis kuni ühtsuseni miinusega. Kui 8 asemel võtame jagatis 9, siis lubame ka vea, mis on väiksem kui üks, kuna me ei liida kogu ühikut, vaid 2/3. Selline privaatne tahe ligikaudne jagatis ühe piires ülejäägiga.
Võtame nüüd teise näite. Oletame, et peame jagama 27 8-ga. Kuna siin ei saa me täpset täisarvuna väljendatud jagatist, otsime ligikaudset jagatist:
27: 8 = 3 ja ülejäänud 3.
Siin on viga võrdne 3/8, see on väiksem kui üks, mis tähendab, et ligikaudne jagatis (3) leiti täpsusega ühele, millel on puudus. Jätkame jagamist: jagame ülejäänud 3 kümnendikku, saame 30 kümnendikku; jagage need 8-ga.
Kümnendike asemel saime jagatis 3 ja ülejäänu 6 kümnendikku. Kui piirduda arvuga 3,3 ja jätta kõrvale 6, siis lubame viga alla kümnendiku. Miks? Sest täpse jagatise saaks, kui 3,3-le liidame 6 kümnendiku 8-ga jagamise tulemuse; see jaotus annaks tulemuseks 6/80, mis on alla kümnendiku. (Kontrolli!) Seega, kui jagatis piirdume kümnendikutega, siis võime öelda, et oleme jagatise leidnud kümnendiku täpsusega(miinusega).
Jätkame jagamist, et leida teine komakoht. Selleks jagame 6 kümnendikku sajandikuteks ja saame 60 sajandikku; jagage need 8-ga.

Kolmanda koha jagatis osutus 7 ja ülejäänud 4 sajandikku; kui me need ära jätame, lubame viga alla ühe sajandiku, sest 4 sajandikku jagatud 8-ga on väiksem kui üks sajandik. Sellistel juhtudel öeldakse, et jagatis on leitud sajandiku täpsusega(miinusega).
Praegu vaadeldavas näites saame täpse jagatise väljendatuna kümnendmurruna. Selleks piisab, kui jagada viimane jääk, 4 sajandikku, tuhandeteks ja jagada 8-ga.
Kuid valdaval enamusel juhtudel on täpset jagatist võimatu saada ja tuleb piirduda selle ligikaudsete väärtustega. Vaatame nüüd seda näidet:
40: 7 = 5,71428571...
Arvu lõppu paigutatud punktid näitavad, et jagamine pole lõpetatud, st võrdsus on ligikaudne. Tavaliselt kirjutatakse ligikaudne võrdsus järgmiselt:
40: 7 = 5,71428571.
Võtsime jagatise kaheksa kohta pärast koma. Aga kui nii suurt täpsust ei nõuta, võite piirduda ainult kogu jagatise osaga, st arvuga 5 (täpsemalt 6); suurema täpsuse huvides võiks arvesse võtta kümnendikke ja võtta jagatis 5,7; kui see täpsus on mingil põhjusel ebapiisav, võite peatuda sajandikutel ja võtta 5,71 jne. Kirjutame välja üksikud jagatised ja nimetame need.
Esimene ligikaudne jagatis, mille täpsus on üks 6.
Teine » » » kümnendikuni 5.7.
Kolmas » » » ühe sajandikuni 5.71.
Neljas » » » ühe tuhandikuni 5,714.
Seega, et leida ligikaudne jagatis, mis on täpne mõne, näiteks 3. kümnendkoha täpsusega (st kuni ühe tuhandikuni), lõpetage jagamine kohe, kui see märk on leitud. Sel juhul peate meeles pidama §-s 40 sätestatud reeglit.
§ 113. Lihtsamad protsente puudutavad ülesanded.
Pärast kümnendkohtade tundmaõppimist teeme veel mõned protsendiülesanded.
Need probleemid on sarnased nendega, mida lahendasime fraktsioonide osakonnas; kuid nüüd kirjutame sajandikud kümnendmurdude kujul, st ilma selgelt määratud nimetajata.
Esiteks peate suutma hõlpsalt liikuda tavalisest murrust kümnendkohani, mille nimetaja on 100. Selleks peate jagama lugeja nimetajaga:

Allolevas tabelis on näidatud, kuidas % (protsent) sümboliga arv asendatakse kümnendmurruga, mille nimetaja on 100:

Vaatleme nüüd mitmeid probleeme.
1. Antud arvu protsendi leidmine.
Ülesanne 1.Ühes külas elab vaid 1600 inimest. Laste arv koolieas moodustab 25% elanike koguarvust. Kui palju on selles külas kooliealisi lapsi?
Selles ülesandes peate leidma 25% ehk 0,25 1600-st. Ülesanne lahendatakse korrutamisega:
1600 0,25 = 400 (lapsed).
Seetõttu on 25% 1600-st 400.
Selle ülesande selgeks mõistmiseks on kasulik meenutada, et iga saja elanikkonna kohta on 25 kooliealist last. Seetõttu saate kõigi kooliealiste laste arvu leidmiseks esmalt välja selgitada, mitu sadu on arvus 1600 (16), ja seejärel korrutada 25 sadade arvuga (25 x 16 = 400). Nii saate kontrollida lahenduse kehtivust.
2. ülesanne. Hoiupangad annavad hoiustajatele aastas 2% tootlust. Kui palju tulu saab hoiustaja aastas, kui ta paneb kassasse: a) 200 rubla? b) 500 rubla? c) 750 rubla? d) 1000 rubla?
Kõik neli juhtumit Probleemi lahendamiseks peate arvutama 0,02 näidatud summadest, st kõik need numbrid tuleb korrutada 0,02-ga. Teeme seda:
a) 200 0,02 = 4 (rub.),
b) 500 0,02 = 10 (rub.),
c) 750 0,02 = 15 (rub.),
d) 1000 0,02 = 20 (rub.).
Kõiki neid juhtumeid saab kontrollida järgmiste kaalutlustega. Hoiupangad annavad investoritele 2% tulu, s.o 0,02 hoiustesse hoiustatud summast. Kui summa oleks 100 rubla, siis 0,02 sellest oleks 2 rubla. See tähendab, et iga sada toob investorile 2 rubla. tulu. Seetõttu piisab igal vaadeldaval juhul sellest, kui välja mõelda, mitu sadu antud arvus on, ja korrutada 2 rubla selle arvuga sadadega. Näites a) on 2 sadu, mis tähendab
2 2 = 4 (hõõru).
Näites d) on 10 sadu, mis tähendab
2 10 = 20 (hõõru).
2. Arvu leidmine selle protsendi järgi.
Ülesanne 1. Kevadel lõpetas koolis 54 õpilast, mis moodustab 6% kooli õpilastest. Kui palju õpilasi eelmisel aastal koolis oli? õppeaasta?
Teeme kõigepealt selgeks selle ülesande tähenduse. Kooli lõpetas 54 õpilast, mis moodustab 6% õpilaste üldarvust ehk teisisõnu 6 sajandikku (0,06) kõigist kooli õpilastest. See tähendab, et teame õpilaste osa, mis on väljendatud arvuga (54) ja murdosaga (0,06) ning sellest murdosast peame leidma täisarvu. Seega on meie ees tavaline ülesanne leida arv selle murdosa hulgast (§90, lõige 6). Seda tüüpi probleemid lahendatakse jagamise teel:
See tähendab, et koolis oli ainult 900 õpilast.
Selliseid ülesandeid on kasulik kontrollida pöördülesande lahendamisega, s.t pärast ülesande lahendamist tuleks vähemalt oma peas lahendada esimest tüüpi ülesanne (antud arvu protsendi leidmine): võtke leitud arv ( 900) antud kujul ja leidke lahendatud ülesandes näidatud protsent sellest, nimelt:
900 0,06 = 54.
2. ülesanne. Perekond kulutab kuu jooksul toidule 780 rubla, mis on 65%. igakuine töötasu isa. Määrake tema igakuine sissetulek.
Sellel ülesandel on sama tähendus kui eelmisel. See annab osa igakuisest töötasust, väljendatuna rublades (780 rubla), ja näitab, et see osa moodustab 65% ehk 0,65 kogupalgast. Ja see, mida te otsite, on kogu tulu:
780: 0,65 = 1 200.
Seetõttu on nõutav sissetulek 1200 rubla.
3. Arvude protsendi leidmine.
Ülesanne 1. IN kooli raamatukogu ainult 6000 raamatut. Nende hulgas on 1200 matemaatikateemalist raamatut. Kui suur protsent matemaatikaraamatutest moodustab raamatukogus olevate raamatute koguarvu?
Oleme juba kaalunud (§97) sedalaadi probleeme ja jõudnud järeldusele, et kahe arvu protsendi arvutamiseks tuleb leida nende arvude suhe ja korrutada see 100-ga.
Meie ülesandes peame leidma arvude 1200 ja 6000 protsentuaalse suhte.
Leiame esmalt nende suhte ja seejärel korrutame selle 100-ga:
![]()
Seega on arvude 1200 ja 6000 osakaal 20. Ehk siis matemaatikaraamatud moodustavad 20% kõigi raamatute koguarvust.
Kontrollimiseks lahendame pöördülesande: leidke 20% 6000-st:
6 000 0,2 = 1 200.
2. ülesanne. Tehas peaks saama 200 tonni kivisütt. 80 tonni on juba tarnitud Mitu protsenti kivisütt on tehasesse tarnitud?
See ülesanne küsib, mitu protsenti on üks arv (80) teisest (200). Nende arvude suhe on 80/200. Korrutame selle 100-ga:
![]()
See tähendab, et 40% kivisöest on tarnitud.
Ristkülik?
Lahendus. Kuna 2,88 dm2 = 288 cm2 ja 0,8 dm = 8 cm, siis on ristküliku pikkus 288: 8, see tähendab 36 cm = 3,6 dm. Leidsime sellise arvu 3,6, et 3,6 0,8 = 2,88. See on jagatis 2,88 jagatud 0,8-ga.
Nad kirjutavad: 2,88: 0,8 = 3,6.
Vastuse 3.6 saab ilma detsimeetrit sentimeetriteks teisendamata. Selleks tuleb jagaja 0,8 ja dividend 2,88 korrutada 10-ga (see tähendab, nihutada koma ühe koha võrra paremale) ja jagada 28,8 8-ga. Jällegi saame: 28,8: 8 = 3,6.
Arvu kümnendmurruga jagamiseks peate:
1) nihutada dividendis ja jagajas koma paremale nii mitme numbri võrra, kui palju on jagajas pärast koma;
2) pärast seda jagage naturaalarvuga.
Näide 1. Jagage 12,096 2,24-ga. Liigutage koma dividendis ja jagage 2 numbrit paremale. Saame arvud 1209,6 ja 224. Kuna 1209,6: 224 = 5,4, siis 12,096: 2,24 = 5,4.
Näide 2. Jagage 4,5 0,125-ga. Siin peate nihutama dividendi koma ja jagama 3 numbrit paremale. Kuna dividendil on pärast koma ainult üks koht, siis lisame sellest paremale kaks nulli. Pärast koma liigutamist saame numbrid 4500 ja 125. Kuna 4500: 125 = 36, siis 4,5: 0,125 = 36.
Näidetest 1 ja 2 on selge, et arvu jagamisel valemurruga see arv väheneb või ei muutu ning korraliku kümnendmurruga jagamisel suureneb: 12,096 > 5,4 ja 4,5< 36.
Jagage 2,467 0,01-ga. Pärast dividendi ja jagaja koma nihutamist 2 numbriga paremale, leiame, et jagatis võrdub 246,7: 1, see tähendab 246,7.
See tähendab 2,467: 0,01 = 246,7. Siit saame reegli:
Kümnendkoha jagamiseks 0,1; 0,01; 0,001, peate selles olevat koma nihutama paremale nii mitme numbri võrra, kui jagajas on ühe ees nullid (st korrutage see 10, 100, 1000-ga).
Kui numbreid pole piisavalt, tuleb need esmalt lõpus lisada fraktsioonid paar nulli.
Näiteks 56,87: 0,0001 = 56,8700: 0,0001 = 568 700.
Sõnastage kümnendmurru jagamise reegel: kümnendmurruga; 0,1 võrra; 0,01; 0,001.
Millise arvuga korrutades saab asendada jagamise 0,01-ga?
1443. Leidke jagatis ja kontrollige korrutamisega:
a) 0,8: 0,5; b) 3,51: 2,7; c) 14,335: 0,61.
1444. Leidke jagatis ja kontrollige jagamise teel:
a) 0,096: 0,12; b) 0,126: 0,9; c) 42,105: 3,5.
a) 7,56: 0,6; g) 6,944: 3,2; n) 14,976: 0,72;
b) 0,161: 0,7; h) 0,0456: 3,8; o) 168,392: 5,6;
c) 0,468: 0,09; i) 0,182: 1,3; n) 24,576: 4,8;
d) 0,00261: 0,03; j) 131,67: 5,7; p) 16,51: 1,27;
e) 0,824: 0,8; l) 189,54: 0,78; c) 46,08: 0,384;
e) 10,5: 3,5; m) 636: 0,12; t) 22,256: 20,8.
1446. Kirjutage üles väljendid:
a) 10 - 2,4x = 3,16; e) 4,2р - р = 5,12;
b) (y + 26,1) 2,3 = 70,84; e) 8,2t - 4,4t = 38,38;
c) (z - 1,2): 0,6 = 21,1; g) (10,49 - s): 4,02 = 0,805;
d) 3,5 m + t = 9,9; h) 9k - 8,67k = 0,6699.
1460. Kahes paagis oli 119,88 tonni bensiini. Esimene paak sisaldas 1,7 korda rohkem bensiini kui teine. Kui palju bensiini igas paagis oli?
1461. Kolmelt krundilt koguti kapsast 87,36 tonni. Samal ajal koguti esimeselt proovitükilt 1,4 korda rohkem, teiselt 1,8 korda rohkem kui kolmandalt. Mitu tonni kapsast igalt krundilt koguti?
1462. Känguru on 2,4 korda lühem kui kaelkirjak ja kaelkirjak on 2,52 m kõrgem kui kaelkirjak Kui kõrge on kaelkirjak ja kui suur on känguru?
1463. Kaks jalakäijat olid üksteisest 4,6 km kaugusel. Nad läksid üksteisele vastu ja kohtusid 0,8 tunni pärast Leia iga jalakäija kiirus, kui ühe kiirus on teise 1,3 korda suurem.
1464. Järgige neid samme.
a) (130,2–30,8): 2,8–21,84:
b) 8,16: (1,32 + 3,48) - 0,345;
c) 3,712: (7 - 3,8) + 1,3 (2,74 + 0,66);
d) (3,4: 1,7 + 0,57: 1,9) 4,9 + 0,0825: 2,75;
e) (4,44: 3,7 - 0,56: 2,8): 0,25 - 0,8;
e) 10,79: 8,3 0,7 - 0,46 3,15: 6,9.
1465. Esitage murd kümnendkohana ja leidke väärtus väljendid:

1466. Arvuta suuliselt:
a) 25,5: 5; b) 9 0,2; c) 0,3:2; d) 6,7 - 2,3;
1,5: 3; 1 0,1; 2:5; 6- 0,02;
4,7: 10; 16 0,01; 17,17: 17; 3,08 + 0,2;
0,48: 4; 24 0,3; 25,5: 25; 2,54 + 0,06;
0,9:100; 0,5 26; 0,8:16; 8,2-2,2.
1467. Leia töö:
a) 0,1 0,1; d) 0,4 0,4; g) 0,7 0,001;
b) 1,3 1,4; e) 0,06 0,8; h) 100 0,09;
c) 0,3 0,4; e) 0,01 100; i) 0,3 0,3 0,3.
1468. Leia: 0,4 arvust 30; 0,5 arvust 18; 0,1 numbrid 6,5; 2,5 numbrid 40; 0,12 number 100; 0,01 arvust 1000.
1469. Mis on avaldise 5683.25a väärtus, kui a = 10; 0,1; 0,01; 100; 0,001; 1000; 0,00001?
1470. Mõelge, millised arvud võivad olla täpsed ja millised ligikaudsed:
a) klassis on 32 õpilast;
b) kaugus Moskvast Kiievisse on 900 km;
c) rööptahukal on 12 serva;
d) laua pikkus 1,3 m;
e) Moskva elanikkond on 8 miljonit inimest;
e) kotis 0,5 kg jahu;
g) Kuuba saare pindala on 105 000 km2;
h) kooli raamatukogus on 10 000 raamatut;
i) üks vahemik võrdub 4 vershokiga ja vershok on võrdne 4,45 cm (vershok
falanksi pikkus nimetissõrm).
1471. Leidke ebavõrdsusele kolm lahendust:
a) 1.2< х < 1,6; в) 0,001 < х < 0,002;
b) 2.1< х< 2,3; г) 0,01 <х< 0,011.
1472. Võrrelge ilma arvutamata avaldiste väärtusi:
a) 24 0,15 ja (24-15): 100;
b) 0,084 0,5 ja (84 5): 10 000.
Selgitage oma vastust.
1473. Ümardage arvud:

1474. Tehke jagamine:
a) 22,7: 10; 23,3:10; 3.14:10; 9,6:10;
b) 304: 100; 42,5: 100; 2,5: 100; 0,9: 100; 0,03: 100;
c) 143,4: 12; 1,488: 124; 0,3417: 34; 159,9: 235; 65,32: 568.
1475. Külast lahkus jalgrattur kiirusega 12 km/h. 2 tunni pärast lahkus samast külast teine jalgrattur vastassuunas,
ja teise kiirus on 1,25 korda suurem kui esimese kiirus. Kui suur on nende vahemaa 3,3 tundi pärast teise jalgratturi lahkumist?
1476. Paadi enda kiirus on 8,5 km/h, hoovuse kiirus 1,3 km/h. Kui kaugele sõidab paat allavoolu 3,5 tunniga? Kui kaugele läbib paat vastuvoolu 5,6 tunniga?
1477. Tehas tootis 3,75 tuhat osa ja müüs need hinnaga 950 rubla. tükk. Tehase kulutused ühe osa tootmiseks moodustasid 637,5 rubla. Leidke nende osade müügist saadav kasum.
1478. Ristkülikukujulise rööptahuka laius on 7,2 cm, mis on ![]() Leidke selle rööptahuka ruumala ja ümardage vastus täisarvudeni.
Leidke selle rööptahuka ruumala ja ümardage vastus täisarvudeni.
1479. Papa Carlo lubas anda Pierole iga päev 4 soldiit ja Buratinole esimesel päeval 1 soldi ja igal järgneval päeval 1 soldi rohkem, kui ta hästi käitub. Pinocchio solvus: ta otsustas, et ükskõik kui palju ta ka ei pingutaks, ei saa ta kunagi nii palju soldatit kui Pierrot. Mõelge, kas Pinocchiol on õigus.
1480. 3 kapi ja 9 raamaturiiuli jaoks kulus 231 m laudu ning kapi jaoks kulub 4 korda rohkem materjali kui riiuli jaoks. Mitu meetrit laudu läheb kapile ja kui palju riiulile?
1481. Lahendage ülesanne:
1) Esimene number on 6,3 ja moodustab teise numbri. Kolmas number moodustab teise. Leidke teine ja kolmas number.
2) Esimene number on 8,1. Teine number pärineb esimesest ja kolmandast numbrist. Leidke teine ja kolmas number.
1482. Leia väljendi tähendus:
1) (7 - 5,38) 2,5;
2) (8 - 6,46) 1,5.
1483. Leia jagatise väärtus:
a) 17.01: 6.3; d) 1,4245: 3,5; g) 0,02976: 0,024;
b) 1,598: 4,7; e) 193,2: 8,4; h) 11,59: 3,05;
c) 39,156: 7,8; e) 0,045: 0,18; i) 74,256: 18,2.
1484. Kodu ja kooli kaugus on 1,1 km. Tüdruk läbib selle tee 0,25 tunniga Kui kiiresti tüdruk kõnnib?
1485. Kahetoalises korteris on ühe toa pind 20,64 m2 ja teise toa pind 2,4 korda väiksem. Leidke nende kahe ruumi pindala koos.
1486. Mootor kulutab 7,5 tunniga 111 liitrit kütust. Mitu liitrit kütust kulutab mootor 1,8 tunni jooksul?
1487. Metalldetail mahuga 3,5 dm3 on massiga 27,3 kg. Teise samast metallist valmistatud detaili mass on 10,92 kg. Kui suur on teise osa maht?
1488. Kahe toru kaudu valati paaki 2,28 tonni bensiini. Läbi esimese toru voolas tunnis 3,6 tonni bensiini ja see oli avatud 0,4 tundi.Teisest torust voolas 0,8 tonni bensiini tunnis vähem kui läbi esimese. Kui kaua teine toru lahti oli?
1489. Lahenda võrrand:
a) 2,136: (1,9 - x) = 7,12; c) 0,2t + 1,7t - 0,54 = 0,22;
b) 4,2 (0,8 + y) = 8,82; d) 5,6 g - 2z - 0,7 z + 2,65 = 7.
1490. Kaup kaaluga 13,3 tonni jaotati kolme sõiduki vahel. Esimest autot lasti 1,3 korda rohkem ja teist autot 1,5 korda rohkem kui kolmandat autot. Mitu tonni kaupa laaditi igale sõidukile?
1491. Kaks jalakäijat lahkusid samast kohast korraga vastassuundades. 0,8 tunni pärast oli nende vahe 6,8 km. Ühe jalakäija kiirus oli 1,5 korda suurem kui teise. Leidke iga jalakäija kiirus.
1492. Järgige neid samme.
a) (21,2544: 0,9 + 1,02 3,2): 5,6;
b) 4,36: (3,15 + 2,3) + (0,792 - 0,78) 350;
c) (3,91: 2,3 5,4 - 4,03) 2,4;
d) 6,93: (0,028 + 0,36 4,2) - 3,5.
1493. Kooli tuli arst ja tõi vaktsineerimiseks 0,25 kg seerumit. Kui paljudele meestele saab ta süstida, kui iga süsti jaoks on vaja 0,002 kg seerumit?
1494. Poodi toimetati 2,8 tonni piparkooke. Enne lõunat müüdi neid piparkooke. Mitu tonni piparkooke jääb müüki?
1495. Kangatükist lõigati 5,6 m Mitu meetrit kangast oli tükis, kui see tükk ära lõigata?
N.Ya. VILENKIN, V. I. ŽOHOV, A. S. TŠESNOKOV, S. I. ŠVARTSBURD, matemaatika 5. klass, Õpik üldharidusasutustele