Selles artiklis vaatleme sellist olulist kümnendarvuga toimingut nagu jagamine. Kõigepealt sõnastame üldised põhimõtted, siis vaatame, kuidas kümnendmurde õigesti veergude kaupa jagada nii teiste murdude kui ka naturaalarvudega. Järgmisena analüüsime tavaliste murdude jagamist kümnendkohtadeks ja vastupidi ning lõpus vaatame, kuidas õigesti jagada murde, mis lõpevad numbritega 0, 1, 0, 01, 100, 10 jne.
Siin võtame ainult positiivsete murdudega juhtumeid. Kui murru ees on miinus, siis sellega opereerimiseks tuleb uurida materjali ratsionaal- ja reaalarvude jagamise kohta.
Yandex.RTB R-A-339285-1
Kõik kümnendmurrud, nii lõplikud kui ka perioodilised, on õiglased eriline vorm harilike murdude kirjutamine. Järelikult kehtivad neile samad põhimõtted, mis nende vastavate tavaliste murdude suhtes. Seega taandame kogu kümnendmurdude jagamise protsessi nende asendamisele tavalistega, millele järgneb arvutamine meile juba tuntud meetoditega. Võtame konkreetse näite.
Näide 1
Jagage 1,2 0,48-ga.
Lahendus
Kirjutame kümnendmurrud tavalisteks murrudeks. Me saame:
1 , 2 = 12 10 = 6 5
0 , 48 = 48 100 = 12 25 .
Seega peame 6 5 jagama 12 25-ga. Me arvestame:
1, 2: 0, 48 = 6 2: 12 25 = 6 5 25 12 = 6 25 5 12 = 5 2
Saadud valest murrust saate valida terve osa ja saada segaarvu 2 1 2 või esitada selle kümnendmurruna, nii et see vastaks algarvudele: 5 2 = 2, 5. Oleme juba varem kirjutanud, kuidas seda teha.
Vastus: 1 , 2: 0 , 48 = 2 , 5 .
Näide 2
Arvutage, kui palju on 0, (504) 0, 56.
Lahendus
Kõigepealt peame perioodika tõlkima kümnend tavaliseks.
0 , (504) = 0 , 504 1 - 0 , 001 = 0 , 504 0 , 999 = 504 999 = 56 111
Pärast seda teisendame ka lõpliku kümnendmurru teisele kujule: 0, 56 = 56 100. Nüüd on meil kaks numbrit, mille abil on meil lihtne vajalikke arvutusi teha:
0 , (504) : 1 , 11 = 56 111: 56 100 = 56 111 100 56 = 100 111
Meil on tulemus, mille saame teisendada ka kümnendvormingusse. Selleks jagage lugeja veerumeetodil nimetajaga:
Vastus: 0 , (504) : 0 , 56 = 0 , (900) .
Kui jagamisnäites kohtasime mitteperioodilisi kümnendmurde, siis toimime veidi teisiti. Me ei saa neid taandada tavalisteks tavalisteks murdudeks, seega peame jagamisel need esmalt ümardama teatud numbrini. Seda toimingut tuleb teha nii dividendi kui ka jagajaga: täpsuse huvides ümardame ka olemasoleva lõpliku või perioodilise murru.
Näide 3
Leidke, kui palju on 0,779... / 1,5602.
Lahendus
Esiteks ümardame mõlemad murrud lähima sajandikuni. Nii liigume lõpmatute mitteperioodiliste murdude juurest lõplike kümnendmurdude juurde:
0 , 779 … ≈ 0 , 78
1 , 5602 ≈ 1 , 56
Saame arvutusi jätkata ja saame ligikaudse tulemuse: 0, 779 ...: 1, 5602 ≈ 0, 78: 1, 56 = 78 100: 156 100 = 78 100 100 156 = 78 156 = 1 5 = 0,.
Tulemuse täpsus sõltub ümardamise astmest.
Vastus: 0 , 779 … : 1 , 5602 ≈ 0 , 5 .
Kuidas jagada naturaalarvu kümnendkohaga ja vastupidi
Jagamise lähenemisviis on sel juhul peaaegu sama: lõplikud ja perioodilised murrud asendame tavalistega ning lõpmatud mitteperioodilised ümardame. Alustame naturaalarvu ja kümnendmurruga jagamise näitega.
Näide 4
Jagage 2,5 45-ga.
Lahendus
Vähendame 2, 5 harilikuks murruks: 255 10 = 51 2. Järgmisena peame selle lihtsalt jagama naturaalarv. Me juba teame, kuidas seda teha:
25, 5: 45 = 51 2: 45 = 51 2 1 45 = 17 30
Kui teisendame tulemuse kümnendarvuks, saame 0,5 (6).
Vastus: 25 , 5: 45 = 0 , 5 (6) .
Pika jagamise meetod on hea mitte ainult naturaalarvude jaoks. Analoogia põhjal saame seda kasutada murdude jaoks. Allpool näitame toimingute jada, mida selleks tuleb teha.
Definitsioon 1
Kümnendmurdude veeru naturaalarvudega jagamiseks vajate:
1. Lisage parempoolsele kümnendmurrule mõned nullid (jagamiseks võime neid lisada suvalise arvu, kui vaja).
2. Jagage kümnendmurd naturaalarvuga, kasutades algoritmi. Kui kogu murruosa jagamine lõpeb, paneme saadud jagatisesse koma ja loeme edasi.
Sellise jagamise tulemuseks võib olla kas lõplik või lõpmatu perioodiline kümnendmurd. See sõltub jäägist: kui see on null, on tulemus lõplik ja kui jäägid hakkavad korduma, on vastuseks perioodiline murd.
Võtame näitena mitu ülesannet ja proovime neid samme konkreetsete numbritega läbi viia.
Näide 5
Arvutage, kui palju on 65, 14 4.
Lahendus
Kasutame veeru meetodit. Selleks lisage murdarvule kaks nulli ja saate kümnendmurru 65, 1400, mis võrdub esialgsega. Nüüd kirjutame veeru 4-ga jagamiseks:
Saadud arv on tulemus, mida vajame täisarvulise osa jagamisel. Me paneme koma, eraldades selle ja jätkame:
Oleme jõudnud nullini, seega on jagamisprotsess lõppenud.
Vastus: 65 , 14: 4 = 16 , 285 .
Näide 6
Jagage 164,5 27-ga.
Lahendus
Esmalt jagame murdosa ja saame:
Eraldage saadud arv komaga ja jätkake jagamist:
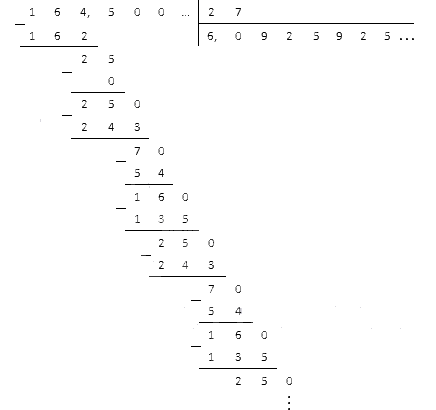
Näeme, et jäägid hakkasid perioodiliselt korduma ja jagatis hakkasid numbrid üheksa, kaks ja viis vahelduma. Siinkohal peatume ja kirjutame vastuse perioodilise murruna 6, 0 (925).
Vastus: 164 , 5: 27 = 6 , 0 (925) .
Seda jagamist saab taandada kümnendmurru ja naturaalarvu jagatise leidmise protsessiks, mida on juba eespool kirjeldatud. Selleks peame korrutama dividendi ja jagaja arvuga 10, 100 jne, nii et jagaja muutuks naturaalarvuks. Järgmisena viime läbi ülalkirjeldatud toimingute jada. Selline lähenemine on võimalik tänu jagamise ja korrutamise omadustele. Panime need kirja järgmiselt:
a: b = (a · 10) : (b · 10) , a: b = (a · 100) : (b · 100) ja nii edasi.
Sõnastame reegli:
2. definitsioon
Ühe viimase kümnendmurru jagamiseks teisega:
1. Liigutage koma dividendis ja jagajas paremale numbrite arvu võrra, mis on vajalikud jagaja naturaalarvuks muutmiseks. Kui dividendis pole piisavalt märke, lisame sellele nullid parem pool.
2. Pärast seda jagage murru veeru võrra saadud naturaalarvuga.
Vaatame konkreetset probleemi.
Näide 7
Jagage 7,287 2,1-ga.
Lahendus: jagaja naturaalarvuks muutmiseks peame nihutama kümnendkoha ühe koha võrra paremale. Nii jätkasime kümnendmurru 72, 87 jagamisega 21-ga. Kirjutame saadud arvud veergu ja arvutame
Vastus: 7 , 287: 2 , 1 = 3 , 47
Näide 8
Arvuta 16.30.021.
Lahendus
Peame koma kolm kohta nihutama. Jagajas pole selleks piisavalt numbreid, mis tähendab, et peate kasutama täiendavaid nulle. Arvame, et tulemus on:
Näeme jääkide 4, 19, 1, 10, 16, 13 perioodilist kordumist. Jagatis korduvad 1, 9, 0, 4, 7 ja 5. Siis on meie tulemuseks perioodiline kümnendmurd 776, (190476).
Vastus: 16 , 3: 0 , 021 = 776 , (190476)
Meie kirjeldatud meetod võimaldab teil teha vastupidist, st jagada naturaalarv viimase kümnendmurruga. Vaatame, kuidas see tehtud on.
Näide 9
Arvutage, kui palju on 3 5, 4.
Lahendus
Ilmselgelt peame koma õigesse kohta nihutama. Pärast seda saame jätkata 30, 0 jagamist 54-ga. Kirjutame andmed veergu ja arvutame tulemuse:
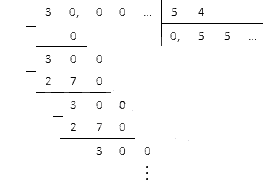
Jääki korrates saame lõpliku arvu 0, (5), mis on perioodiline kümnendmurd.
Vastus: 3: 5 , 4 = 0 , (5) .
Kuidas jagada kümnendkohti 1000, 100, 10 jne.
Juba uuritud harilike murdude jagamise reeglite kohaselt on murdosa jagamine kümnete, sadade, tuhandetega sarnane selle korrutamisele 1/1000, 1/100, 1/10 jne. Selgub, et jagamise läbiviimiseks , sel juhul Liigutage lihtsalt koma vajaliku arvu numbriteni. Kui arvus pole ülekandmiseks piisavalt väärtusi, peate lisama vajaliku arvu nulle.
Näide 10
Niisiis, 56, 21: 10 = 5, 621 ja 0, 32: 100 000 = 0, 0000032.
Lõpmatute kümnendmurdude puhul teeme sama.
Näide 11
Näiteks 3, (56): 1000 = 0, 003 (56) ja 593, 374...: 100 = 5, 93374....
Kuidas jagada kümnendkohti 0,001, 0,01, 0,1 jne.
Sama reeglit kasutades saame jagada ka murde näidatud väärtusteks. See toiming sarnaneb vastavalt 1000, 100, 10-ga korrutamisega. Selleks liigutame koma ühe-, kahe- või kolmekohaliseks, olenevalt ülesande tingimustest ja lisame nullid, kui numbris pole piisavalt numbreid.
Näide 12
Näiteks 5,739: 0,1 = 57,39 ja 0,21: 0,00001 = 21 000.
See reegel kehtib ka lõpmatute kümnendmurdude kohta. Soovitame olla ettevaatlik vastuses kuvatava murdosa perioodiga.
Niisiis, 7, 5 (716) : 0, 01 = 757, (167), sest pärast koma liigutamist kümnendmurrus 7, 5716716716... kaks kohta paremale, saime 757, 167167....
Kui meil on näites mitteperioodilised murrud, siis on kõik lihtsam: 394, 38283...: 0, 001 = 394382, 83....
Kuidas jagada segaarvu või murdosa kümnendkohaga ja vastupidi
Samuti taandame selle toimingu tavaliste murdudega tehtele. Selleks tuleb kümnendarvud asendada vastavate tavaliste murdudega ja kirjutada segaarv valemurruna.
Kui jagame mitteperioodilise murru hariliku või segaarvuga, peame toimima vastupidiselt, asendades hariliku murru või segaarvu vastava kümnendmurruga.
Kui märkate tekstis viga, tõstke see esile ja vajutage Ctrl+Enter
I. Kümnendmurru naturaalarvuga jagamiseks peate murdosa selle arvuga jagama, kuna naturaalarvud jagunevad, ja panema jagatisesse koma, kui kogu osa jagamine on lõpetatud.
Näited.
Tehke jagamine: 1) 96,25: 5; 2) 4,78: 4; 3) 183,06: 45.
Lahendus.
Näide 1) 96,25: 5.
Jagame “nurgaga” samamoodi nagu naturaalarvusid. Pärast seda, kui oleme numbri maha võtnud 2 (kümnendike arv on esimene koht pärast koma dividendis 96, 2 5), jagatisesse paneme koma ja jätkame jagamist.
Vastus: 19,25.
Näide 2) 4,78: 4.
Jagame nii, nagu naturaalarvud jagunevad. Jagatisesse paneme koma kohe pärast selle eemaldamist 7
— dividendi 4 esimene number pärast koma, 7
8. Jätkame jagamist edasi. 38-36 lahutamisel saame 2, kuid jagamist ei lõpetata. Kuidas me edasi toimime? Teame, et kümnendmurru lõppu saab lisada nulle – see ei muuda murru väärtust. Määrame nulli ja jagame 20 4-ga. Saame 5 - jagamine on lõppenud.
Vastus: 1,195.
Näide 3) 183,06: 45.
Jagage 18306 45-ga. Jagatisesse paneme koma kohe pärast numbri eemaldamist 0
— esimene number pärast koma dividendis 183, 0
6. Nii nagu näites 2), pidime arvule 36 määrama nulli – arvude 306 ja 270 vahe.
Vastus: 4,068.
Järeldus: kümnendmurru jagamisel naturaalarvuga privaatne panime koma kohe pärast seda, kui võtame maha dividendi kümnendiku koha näitaja. Pange tähele: kõik on esile tõstetud numbrid punaselt nendes kolmes näites kuuluvad kategooriasse kümnendikku dividendist.
II. Kümnendmurru jagamiseks 10, 100, 1000 jne võrra tuleb koma nihutada 1, 2, 3 jne numbri võrra vasakule.
Näited.
Tehke jaotus: 1) 41,56: 10; 2) 123,45: 100; 3) 0,47: 100; 4) 8,5: 1000; 5) 631,2: 10000.
Lahendus.
Kümnendkoha liigutamine vasakule sõltub sellest, mitu nulli pärast ühte on jagajas. Niisiis, kümnendmurru jagamisel 10
kanname dividendina üle koma vasakule ühele numbrile; kui jagatud 100
- liigutage koma jäänud kaks numbrit; kui jagatud 1000
teisendada selle kümnendmurruks koma kolm numbrit vasakule.
Kui tundub, et teie laps ei saa aru, kuidas kümnendkohti jagada, pole see põhjust arvata, et ta pole matemaatikas võimeline.
Tõenäoliselt ei selgitanud nad talle lihtsalt selgelt, kuidas seda tehti. Peame last aitama ja rääkima talle murdudest ja nendega tehtavatest tehingutest võimalikult lihtsal, peaaegu mängulisel viisil. Ja selleks peame me ise midagi meeles pidama.
Murdlauseid kasutatakse siis, kui me räägime mittetäisarvude kohta. Kui murdosa on väiksem kui üks, siis kirjeldab see osa millestki, kui on rohkem, siis mitut tervet osa ja teist tükki. Murdu kirjeldatakse kahe väärtusega: nimetaja, mis selgitab, kui palju võrdsetes osades Arv jagatakse lugejaga, mis annab meile teada, mitut sellist osa me silmas peame.
Oletame, et lõikasite piruka 4 võrdseks osaks ja andsite neist ühe oma naabritele. Nimetaja on 4. Ja lugeja oleneb sellest, mida me kirjeldada tahame. Kui me räägime sellest, kui palju naabritele anti, siis on lugeja 1 ja kui me räägime sellest, kui palju jäi, siis 3.
Piruka näites on nimetajaks 4 ja avaldises “1 päev on 1/7 nädalast” on see 7. Mis tahes nimetajaga murdosa avaldis on harilik murd.
Matemaatikud, nagu kõik teisedki, püüavad oma elu lihtsamaks teha. Ja sellepärast leiutati kümnendmurrud. Nendes on nimetaja võrdne 10-ga või arvudega, mis on 10-kordsed (100, 1000, 10 000 jne) ja need on kirjutatud järgmiselt: arvu täisarvuline komponent eraldatakse murdosast komaga. Näiteks 5,1 on 5 tervet ja 1 kümnendikku ning 7,86 on 7 tervet ja 86 sajandikku.
Väike retriit ei ole teie lastele, vaid teile endale. Meie riigis on tavaks eraldada murdosa komaga. Välismaal on väljakujunenud traditsiooni kohaselt tavaks eraldada see punktiga. Seetõttu ärge imestage, kui kohtate võõras tekstis sarnast märgistust.
Murdude jagamine
Igal sarnaste arvudega aritmeetilisel toimingul on oma omadused, kuid nüüd proovime õppida, kuidas kümnendmurde jagada. Murru on võimalik jagada naturaalarvuga või mõne muu murruga.
Selle aritmeetilise tehte valdamise hõlbustamiseks on oluline meeles pidada üht lihtsat asja.
Kui olete õppinud kasutama komasid, saate kasutada samu jagamisreegleid, mis täisarvude puhul.
Kaaluge murdosa jagamist naturaalarvuga. Veeruks jagamise tehnoloogia peaks olema teile juba varem kaetud materjalist teada. Menetlus on sarnane. Dividend jagab märk märgi haaval jagajaga. Niipea, kui pööre jõuab viimase märgini enne koma, pannakse jagatisesse koma ja seejärel toimub jagamine tavapärasel viisil.
See tähendab, et peale koma eemaldamise on see kõige levinum jaotus ja koma pole eriti keeruline.
Murru jagamine murdosaga
Näited, kus peate jagama ühe murdarvu teisega, tunduvad väga keerulised. Kuid tegelikult pole nendega raskem toime tulla. Ühe kümnendmurru jagamine teisega on palju lihtsam, kui vabaneda jagaja komast.
Kuidas seda teha? Kui teil on vaja panna 90 pliiatsit 10 karpi, siis mitu pliiatsit on igas karbis? 9. Korrutame mõlemad arvud 10-ga – 900 pliiatsi ja 100 kastiga. Kui palju kummaski? 9. Sama põhimõte kehtib ka kümnendmurdu jagamisel.
Jagaja kaotab komast üldse ja dividendi koma nihutatakse paremale sama mitme koha võrra, kui oli jagajas varem. Ja siis viiakse läbi tavaline veergudeks jagamine, mida me eespool arutasime. Näiteks:
25,6/6,4 = 256/64 = 4;
10,24/1,6 = 102,4/16 =6,4;
100,725/1,25 =10072,5/125 =80,58.
Dividend tuleb korrutada ja korrutada 10-ga, kuni jagaja muutub täisarv. Seetõttu võivad sellel paremal olla lisanullid.
40,6/0,58 =4060/58=70.
Selles pole midagi halba. Pidage meeles pliiatsidega näidet - vastus ei muutu, kui suurendate mõlemat numbrit võrra sama numberüks kord. Harilikku murru on keerulisem jagada, eriti puudumisel ühised tegurid lugejas ja nimetajas.
Kümnendkohtade jagamine on selles osas palju mugavam. Kõige keerulisem trikk on siin koma mähkimise nipp, kuid nagu nägime, on seda lihtne käsitseda. Kui saate seda oma lapsele edasi anda, õpetate talle kümnendkohti jagama.
Olles selle lihtsa reegli selgeks õppinud, tunneb teie poeg või tütar end matemaatikatundides palju enesekindlamalt ja kes teab, võib-olla hakkab ta selle aine vastu huvi tundma. Matemaatiline mõtteviis avaldub harva varasest lapsepõlvest, mõnikord on vaja tõuget ja huvi.
Aidates last kodutööde tegemisel, ei paranda sa mitte ainult tema õppeedukust, vaid avardad ka tema huvialasid, mille eest ta aja jooksul sulle tänulik on.
Paljud koolilapsed unustavad keskkooli jõudes ära pika jagamise. Arvutid, kalkulaatorid, Mobiiltelefonid ja muud seadmed on meie ellu nii tihedalt sisenenud, et elementaarsed matemaatilised tehted viivad mõnikord stuuporini. Ja kuidas inimesed ilma kõigi nende hüvedeta paarkümmend aastat tagasi hakkama said? Esiteks peate meeles pidama peamised jagamiseks vajalikud matemaatilised mõisted. Niisiis, dividend on arv, mis jagatakse. Jagaja – arv, millega jagatakse. Tulemusena saadud tulemusi nimetatakse jagatiseks. Ribaks jagamiseks kasutage kooloniga sarnast sümbolit - ":" ja veeruks jagamisel ikooni "∟"; seda nimetatakse ka nurgaks.
Samuti tasub meeles pidada, et iga jagamist saab kontrollida korrutamisega. Jagamise tulemuse kontrollimiseks korrutage see lihtsalt jagajaga; tulemuseks peaks olema arv, mis vastab dividendile (a: b=c; seega c*b=a). Nüüd sellest, mis on kümnendmurd. Kümnendmurd saadakse, jagades ühiku arvuga 0,0, 1000 jne. Nende arvude salvestamine ja nendega tehtavad matemaatilised tehted on täpselt samad, mis täisarvude puhul. Kümnendmurdude jagamisel ei pea meeles pidama, kus nimetaja asub. Kõik selgub numbri üleskirjutamisel. Esiteks kirjutatakse täisarv ja pärast koma selle kümnendik, sajandik, tuhandik. Esimene number pärast koma vastab kümnetele, teine sadadele, kolmas tuhandetele jne.
Iga õpilane peaks teadma, kuidas kümnendkohti kümnendkohtadega jagada. Kui nii dividend kui ka jagaja korrutada sama number, siis vastus, st jagatis ei muutu. Kui kümnendmurd korrutada 0,0, 1000 jne, siis täisarvu järel olev koma muudab oma asukohta – see liigub paremale sama arvu numbrite võrra, kui palju on korrutatud arvus nulle. Näiteks kümnendkoha korrutamisel 10-ga liigub koma ühe numbri võrra paremale. 2,9: 6,7 – korrutame nii jagaja kui ka dividendi 100-ga, saame 6,9: 3687. Kõige parem on korrutada nii, et sellega korrutades ei jääks vähemalt ühele arvule (jagajale või dividendile) pärast koma ühtegi numbrit. , st tehke vähemalt üks arv täisarvuks. Veel mõned näited täisarvu järel komade liigutamisest: 9,2: 1,5 = 2492: 2,5; 5,4:4,8 = 5344:74598.
Tähelepanu, kümnendmurd ei muuda oma väärtust, kui paremale küljele lisatakse nullid, näiteks 3,8 = 3,0. Samuti ei muutu murru väärtus, kui nullid numbri lõpust eemaldatakse paremalt: 3,0 = 3,3. Nulle aga numbri keskelt eemaldada ei saa – 3,3. Kuidas jagada veerus kümnendmurdu naturaalarvuga? Kümnendmurru jagamiseks naturaalarvuga veerus tuleb teha vastav märge nurgaga, jagada. Jagatis tuleb täisarvu jagamise lõppedes panna koma. Näiteks 5,4|2 14 7,2 18 18 0 4 4 0Kui dividendinumbri esimene number on jagajast väiksem, kasutatakse järgnevaid numbreid, kuni on võimalik sooritada esimene tegevus.
Sel juhul on dividendi esimene number 1, seda ei saa jagada 2-ga, seega kasutatakse jagamisel korraga kahte numbrit 1 ja 5: 15 jagatakse 2-ga ülejäänud osaga, see osutub jagatiseks 7 ja jääk jääb 1. Seejärel kasutame dividendi järgmist numbrit - 8. Alandame selle 1-ni ja jagame 18 2-ga. Jagatises kirjutame üles arvu 9. Ülejäägis ei jää midagi, seega kirjutame 0. Alandame järelejäänud dividendi arvu 4 alla ja jagame jagajaga, s.o 2-ga. Jagatises kirjutame üles 2 ja jääk on jälle 0. Selle jagamise tulemuseks on arv 7,2. Seda nimetatakse privaatseks. Kümnendkoha kümnendkohaga jagamise küsimust on üsna lihtne lahendada, kui tead mõnda nippi. Kümnendkohtade mõtteline jagamine on mõnikord üsna keeruline, seetõttu kasutatakse protsessi hõlbustamiseks pikka jagamist.
Selle jagamise korral kehtivad samad reeglid, mis kümnendmurdu täisarvuga jagamisel või stringiks jagamisel. Rea vasakule küljele kirjutavad nad dividendi, seejärel panevad sümboli "nurk" ja seejärel jagaja ning alustavad jagamist. Jagamise hõlbustamiseks ja täisarvu järel oleva koma sobivasse kohta viimiseks võite korrutada kümnete, sadade või tuhandetega. Näiteks 9,2: 1,5 = 24920: 125. Tähelepanu, mõlemad murrud korrutatakse 0,0 1000-ga. Kui dividend korrutati 10-ga, siis korrutatakse ka jagaja 10-ga. B selles näites nii dividend kui ka jagaja korrutati 100-ga. Järgmisena tehakse arvutus samamoodi, nagu on näidatud kümnendmurru naturaalarvuga jagamise näites. 0,1-ga jagamiseks; 0,1; 0,1 jne on vaja nii jagaja kui ka dividend korrutada 0,0, 1000-ga.
Üsna sageli saadakse jagatisega jagamisel, st vastuses, lõpmatuid murde. Sel juhul on vaja arv ümardada kümnendikku, sajandikku või tuhandikku. Sel juhul kehtib reegel: kui pärast arvu, milleni vastus tuleb ümardada, on väiksem või võrdne 5-ga, siis vastus ümardatakse alla, aga kui see on suurem kui 5, siis ümardatakse üles. Näiteks soovite tulemuse 5,5 ümardada tuhandikuteks. See tähendab, et vastus pärast koma peaks lõppema numbriga 6. Pärast 6 on 9, mis tähendab, et ümardame vastuse üles ja saame 5,7. Aga kui vastust 5.5 oleks vaja ümardada mitte tuhandikuteks, vaid kümnenditeks, siis näeks vastus välja selline - 5.2. Sel juhul ei ümardatud 2 üles, kuna sellele järgneb 3 ja see on väiksem kui 5.
§ 107. Kümnendmurdude liitmine.Kümnendkohtade lisamine on sama, mis täisarvude liitmine. Vaatame seda näidetega.
1) 0,132 + 2,354. Märgistame terminid üksteise alla.
Siin saadi 2 tuhandiku liitmisel 4 tuhandikule 6 tuhandikku;
3 sajandiku liitmisel 5 sajandikuga on tulemuseks 8 sajandikku;
1 kümnendiku liitmisest 3 kümnendikuga -4 kümnendikku ja
0 täisarvu lisamisest 2 täisarvuga - 2 täisarvu.
2) 5,065 + 7,83.
Teises terminis pole tuhandeid, seega on oluline terminite üksteise järel märgistamisel mitte vigu teha.
3) 1,2357 + 0,469 + 2,08 + 3,90701.
Siin on tuhandikute liitmisel tulemuseks 21 tuhandikku; kirjutasime tuhandete alla 1 ja sajandikutele lisasime 2, nii et sajandikukohas saime järgmised terminid: 2 + 3 + 6 + 8 + 0; kokku annavad 19 sajandikku, meie kirjutasime alla 9 sajandikku ja 1 arvestati kümnendikku jne.
Seega tuleb kümnendmurdude lisamisel järgida järgmist järjekorda: märgi murrud üksteise alla nii, et kõikides terminites paikneksid üksteise all samad numbrid ja kõik komad ühes vertikaalses veerus; Mõne termini kümnendkohtadest paremale lisatakse vähemalt mõttes selline arv nulle, et kõik pärast koma olevad liikmed oleksid ühepalju numbritega. Seejärel lisavad nad numbrite kaupa, alustades paremast servast, ja lisavad saadud summas koma samasse vertikaalsesse veergu, kus see nendes terminites asub.
§ 108. Kümnendmurdude lahutamine.
Kümnendkohtade lahutamine toimib samamoodi nagu täisarvude lahutamine. Näitame seda näidetega.
1) 9,87 - 7,32. Märgistame minuendi all oleva alajaotuse nii, et sama numbri ühikud oleksid üksteise all:
2) 16,29 - 4,75. Märgime minuendi all oleva alajaotuse, nagu esimeses näites:
Kümnendike lahutamiseks tuli 6-st võtta üks terve ühik ja jagada see kümnendikku.
3) 14,0213-5,350712. Kirjutame alla minuendi all olevale alajaotusele:
Lahutamine toimus järgmiselt: kuna me ei saa 0-st lahutada 2 miljondikut, siis peaksime pöörama vasakul asuva lähima numbri ehk sajatuhandikesse, kuid sajatuhandiku asemel on ka null, seega võtame 1 kümnetuhandiku. 3 kümnetuhandik ja Me jagame selle sajatuhandikeks, saame 10 sajatuhandikku, millest jätame sajatuhandikesse kategooriasse 9 sajatuhandik ja jagame 1 sajatuhandiku miljoniteks, saame 10 miljondiku. Seega on meil kolmes viimases numbris: miljondik 10, sajatuhandik 9, kümnetuhandik 2. Suurema selguse ja mugavuse huvides (et mitte unustada) on need arvud kirjutatud minuendi vastavate murdarvude kohale. Nüüd saate hakata lahutama. 10 miljondikust lahutame 2 miljondikut, saame 8 miljonit; 9 sajatuhandikest lahutame 1 sajatuhandiku, saame 8 sajatuhandiku jne.
Seega järgitakse kümnendmurdude lahutamisel järgmist järjekorda: märkige minuendi all oleva alajaotuse alla nii, et samad numbrid paikneksid üksteise all ja kõik komad oleksid samas vertikaalses veerus; paremale lisavad nad vähemalt mõttes nii palju nulle minuendis või alamjaotises, et neil oleks sama arv numbreid, seejärel lahutavad nad numbrite kaupa, alustades paremalt poolt ja saadud vahesse panevad koma sama vertikaalne veerg, milles see asub minuendis ja lahutades.
§ 109. Kümnendmurdude korrutamine.
Vaatame mõningaid näiteid kümnendmurdude korrutamisest.
Nende arvude korrutise leidmiseks saame arutleda järgmiselt: kui tegurit suurendada 10 korda, siis on mõlemad tegurid täisarvud ja saame need siis korrutada vastavalt täisarvude korrutamise reeglitele. Kuid me teame, et kui üks teguritest suureneb mitu korda, suureneb toode sama palju. See tähendab, et arv, mis saadakse täisarvuliste tegurite korrutamisel, s.o 28 23-ga, on 10 korda suurem tegelikust korrutisest ja tõelise korrutise saamiseks tuleb leitud korrutist 10 korda vähendada. Seetõttu peate siin üks kord korrutama 10-ga ja üks kord jagama 10-ga, kuid 10-ga korrutamine ja jagamine toimub koma ühe koha võrra paremale ja vasakule nihutades. Seetõttu peate tegema seda: teguris liigutage koma õigesse kohta, see võrdub 23-ga, seejärel peate saadud täisarvud korrutama:
See toode on tegelikust 10 korda suurem. Seetõttu tuleb seda vähendada 10 korda, mille jaoks nihutame koma ühe koha võrra vasakule. Seega saame
28 2,3 = 64,4.
Kontrollimise eesmärgil saab kirjutada kümnendmurru nimetajaga ja sooritada toimingu harilike murdude korrutamise reegli järgi, s.t.
2) 12,27 0,021.
Selle näite erinevus eelmisest seisneb selles, et siin on mõlemad tegurid esitatud kümnendmurdudena. Kuid siin ei pööra me korrutamise käigus tähelepanu komadele, s.t suurendame ajutiselt kordajat 100 korda ja kordajat 1000 korda, mis suurendab korrutist 100 000 korda. Seega, korrutades 1227 21-ga, saame:
1 227 21 = 25 767.
Arvestades, et saadud toode on tegelikust tootest 100 000 korda suurem, peame seda nüüd 100 000 korda vähendama, pannes sellesse õigesti koma, siis saame:
32,27 0,021 = 0,25767.
Kontrollime:
Seega piisab kahe kümnendmurru korrutamiseks komadele tähelepanu pööramata, kui korrutada need täisarvudena ja korrutis eraldada paremal pool komaga nii palju kümnendkohti, kui oli korrutis ja korrutis. kordajas kokku.
Viimase näite tulemuseks oli viie kümnendkohaga korrutis. Kui nii suurt täpsust ei nõuta, ümardatakse kümnendmurd. Ümardamisel peaksite kasutama sama reeglit, mis oli näidatud täisarvude puhul.
§ 110. Korrutamine tabelite abil.
Mõnikord saab kümnendkohtade korrutamist teha tabelite abil. Selleks saab kasutada näiteks neid kahekohaliste arvude korrutustabeleid, mille kirjeldus on antud varem.
1) Korrutage 53 1,5-ga.
Korrutame 53 15-ga. Tabelis on see toode 795. Leidsime toote 53 15-ga, kuid meie teine tegur oli 10 korda väiksem, mis tähendab, et toodet tuleb vähendada 10 korda, st.
53 1,5 = 79,5.
2) Korrutage 5,3 4,7-ga.
Esiteks leiame tabelist korrutise 53 korda 47, see saab olema 2 491. Aga kuna suurendasime kordajat ja kordajat kokku 100 korda, on saadud korrutis 100 korda suurem, kui see peaks olema; seega peame seda toodet 100 korda vähendama:
5,3 4,7 = 24,91.
3) Korrutage 0,53 7,4-ga.
Esiteks leiame tabelist korrutise 53 korda 74; see on 3 922. Aga kuna suurendasime kordajat 100 korda ja kordajat 10 korda, suurenes korrutis 1000 korda; seega peame nüüd seda 1000 korda vähendama:
0,53 7,4 = 3,922.
§ 111. Kümnendmurdude jagamine.
Vaatame kümnendmurdude jagamist järgmises järjekorras:
1. Kümnendmurru jagamine täisarvuga,
1. Jaga kümnendmurd täisarvuga.
1) Jaga 2,46 2-ga.
Jagasime 2-ga kõigepealt terve, siis kümnendiku ja lõpuks sajandikuga.
2) Jaga 32,46 3-ga.
32,46: 3 = 10,82.
Jagasime 3 kümnendikku 3-ga, seejärel hakkasime jagama 2 ühikut 3-ga; kuna dividendi (2) ühikute arv on jagajast (3) väiksem, pidime jagatisesse panema 0; edasi, jäägile võtsime 4 kümnendikku ja jagasime 24 kümnendikku 3-ga; sai jagatis 8 kümnendikku ja jagas lõpuks 6 sajandikku.
3) Jagage 1,2345 5-ga.
1,2345: 5 = 0,2469.
Siin on jagatis esikohal null täisarvu, kuna üks täisarv ei jagu 5-ga.
4) Jaga 13,58 4-ga.
Selle näite eripära on see, et kui saime jagatis 9 sajandikku, avastasime jäägi, mis on võrdne 2 sajandikuga, jagasime selle jäägi tuhandeteks, saime 20 tuhandiku ja lõpetasime jagamise.
Reegel. Kümnendmurru jagamine täisarvuga toimub samamoodi nagu täisarvude jagamine ja saadud jäägid teisendatakse järjest väiksemateks kümnendmurdudeks; Jagamine jätkub, kuni jääk on null.
2. Jaga koma kümnendkohaga.
1) Jaga 2,46 0,2-ga.
Me juba teame, kuidas jagada kümnendmurdu täisarvuga. Mõelgem, kas seda uut jagunemisjuhtumit on võimalik taandada eelmisele? Omal ajal pidasime jagatise märkimisväärseks omaduseks, et see jääb muutumatuks, kui dividend ja jagaja samaaegselt suurenevad või vähenevad sama arv kordi. Kui jagaja oleks täisarv, saaksime meile antud numbreid hõlpsasti jagada. Selleks piisab selle 10-kordsest suurendamisest ja õige jagatise saamiseks on vaja dividendi suurendada sama palju, s.o 10 korda. Seejärel asendatakse nende numbrite jaotus järgmiste numbrite jagamisega:
Lisaks ei ole enam vaja andmetes muudatusi teha.
Teeme selle jaotuse:
Seega 2,46: 0,2 = 12,3.
2) Jaga 1,25 1,6-ga.
Suurendame jagajat (1,6) 10 korda; et jagatis ei muutuks, suurendame dividendi 10 korda; 12 täisarvu ei jagu 16-ga, seega kirjutame jagatisesse 0 ja jagame 125 kümnendikku 16-ga, jagatis saame 7 kümnendikku ja jääk 13. Jagame 13 kümnendikku sajandikuteks, määrates nulli ja jagame 130, sajandikku 16-ga jne. Pange tähele järgmist:
a) kui konkreetses ei ole täisarve, siis kirjutatakse nende asemele null täisarvu;
b) kui pärast dividendi numbri lisamist jäägile saadakse arv, mis jagajaga ei jagu, siis jagatisesse kirjutatakse null;
c) kui pärast dividendi viimase numbri eemaldamist jagamine ei lõpe, siis jagamine jätkub, lisades jäägile nullid;
d) kui dividend on täisarv, siis kümnendmurruga jagamisel suurendatakse seda, lisades sellele nullid.
Seega, arvu kümnendmurruga jagamiseks peate jagaja koma ära jätma ja seejärel suurendama dividendi nii mitu korda, kui palju jagaja selles koma ära jättes suurenes, ning seejärel jagama vastavalt reeglile. kümnendmurru jagamiseks täisarvuga.
§ 112. Ligikaudsed jagatised.
Eelmises lõigus vaatlesime kümnendmurdude jagamist ja kõigis lahendatud näidetes oli jagamine lõpetatud, st saadi täpne jagatis. Enamasti pole aga täpset jagatist võimalik saada, ükskõik kui kaugele jagamist jätkame. Siin on üks selline juhtum: jagage 53 101-ga.
Oleme jagatis juba viis numbrit saanud, kuid jagamine pole veel lõppenud ja pole lootustki, et see kunagi lõppeks, kuna ülejäänus hakkavad meil olema numbrid, mida on juba varem kohatud. Jagatis korduvad ka arvud: on ilmne, et pärast arvu 7 ilmub lõputult arv 5, seejärel 2 jne. Sellistel juhtudel jagamine katkeb ja piirdub jagatise paari esimese numbriga. Seda jagatist nimetatakse lähedased. Näitame näidetega, kuidas jagada jagamist.
Olgu vaja jagada 25 3-ga. Ilmselgelt ei saa sellisest jagamisest täpset jagatist, väljendatuna täis- või kümnendmurruna. Seetõttu otsime ligikaudset jagatist:
25: 3 = 8 ja ülejäänud 1
Ligikaudne jagatis on 8; see on muidugi väiksem kui täpne jagatis, sest seal on jääk 1. Täpse jagatise saamiseks tuleb leitud ligikaudsele jagatisele lisada murd, mis saadakse 1-ga võrdse jäägi jagamisel 3-ga, s.t. , kuni 8; see on murdosa 1/3. See tähendab, et väljendatakse täpne jagatis seganumber 8 1/3. Kuna 1/3 on õige murd, st murd, vähem kui üks, siis lubame selle ära visata viga, mis vähem kui üks. Jagatis 8 saab olema ligikaudne jagatis kuni ühtsuseni miinusega. Kui 8 asemel võtame jagatis 9, siis lubame ka vea, mis on väiksem kui üks, kuna me ei liida kogu ühikut, vaid 2/3. Selline privaatne tahe ligikaudne jagatis ühe piires ülejäägiga.
Võtame nüüd teise näite. Oletame, et peame jagama 27 8-ga. Kuna siin ei saa me täpset täisarvuna väljendatud jagatist, otsime ligikaudset jagatist:
27: 8 = 3 ja ülejäänud 3.
Siin on viga võrdne 3/8, see on väiksem kui üks, mis tähendab, et ligikaudne jagatis (3) leiti täpsusega ühele, millel on puudus. Jätkame jagamist: jagame ülejäänud 3 kümnendikku, saame 30 kümnendikku; jagage need 8-ga.
Kümnendike asemel saime jagatis 3 ja ülejäänu 6 kümnendikku. Kui piirduda arvuga 3,3 ja jätta kõrvale 6, siis lubame viga alla kümnendiku. Miks? Sest täpse jagatise saaks, kui 3,3-le liidame 6 kümnendiku 8-ga jagamise tulemuse; see jaotus annaks tulemuseks 6/80, mis on alla kümnendiku. (Kontrolli!) Seega, kui jagatis piirdume kümnendikutega, siis võime öelda, et oleme jagatise leidnud kümnendiku täpsusega(miinusega).
Jätkame jagamist, et leida teine komakoht. Selleks jagame 6 kümnendikku sajandikuteks ja saame 60 sajandikku; jagage need 8-ga.
Kolmanda koha jagatis osutus 7 ja ülejäänud 4 sajandikku; kui me need ära jätame, lubame viga alla ühe sajandiku, sest 4 sajandikku jagatud 8-ga on väiksem kui üks sajandik. Sellistel juhtudel öeldakse, et jagatis on leitud sajandiku täpsusega(miinusega).
Praegu vaadeldavas näites saame täpse jagatise väljendatuna kümnendmurruna. Selleks piisab, kui jagada viimane jääk, 4 sajandikku, tuhandeteks ja jagada 8-ga.
Kuid valdaval enamusel juhtudel on täpset jagatist võimatu saada ja tuleb piirduda selle ligikaudsete väärtustega. Vaatame nüüd seda näidet:
40: 7 = 5,71428571...
Arvu lõppu paigutatud punktid näitavad, et jagamine pole lõpetatud, st võrdsus on ligikaudne. Tavaliselt kirjutatakse ligikaudne võrdsus järgmiselt:
40: 7 = 5,71428571.
Võtsime jagatise kaheksa kohta pärast koma. Aga kui nii suurt täpsust ei nõuta, võite piirduda ainult kogu jagatise osaga, st arvuga 5 (täpsemalt 6); suurema täpsuse huvides võiks arvesse võtta kümnendikke ja võtta jagatis 5,7; kui see täpsus on mingil põhjusel ebapiisav, võite peatuda sajandikutel ja võtta 5,71 jne. Kirjutame välja üksikud jagatised ja nimetame need.
Esimene ligikaudne jagatis, mille täpsus on üks 6.
Teine » » » kümnendikuni 5.7.
Kolmas » » » ühe sajandikuni 5.71.
Neljas » » » ühe tuhandikuni 5,714.
Seega, et leida ligikaudne jagatis, mis on täpne mõne, näiteks 3. kümnendkoha täpsusega (st kuni ühe tuhandikuni), lõpetage jagamine kohe, kui see märk on leitud. Sel juhul peate meeles pidama §-s 40 sätestatud reeglit.
§ 113. Lihtsamad protsente puudutavad ülesanded.
Pärast kümnendkohtade tundmaõppimist teeme veel mõned protsendiülesanded.
Need probleemid on sarnased nendega, mida lahendasime fraktsioonide osakonnas; kuid nüüd kirjutame sajandikud kümnendmurdude kujul, st ilma selgelt määratud nimetajata.
Esiteks peate suutma hõlpsalt liikuda tavalisest murrust kümnendkohani, mille nimetaja on 100. Selleks peate jagama lugeja nimetajaga:
Allolevas tabelis on näidatud, kuidas % (protsent) sümboliga arv asendatakse kümnendmurruga, mille nimetaja on 100:
Vaatleme nüüd mitmeid probleeme.
1. Antud arvu protsendi leidmine.
Ülesanne 1.Ühes külas elab vaid 1600 inimest. Laste arv koolieas moodustab 25% elanike koguarvust. Kui palju on selles külas kooliealisi lapsi?
Selles ülesandes peate leidma 25% ehk 0,25 1600-st. Ülesanne lahendatakse korrutamisega:
1600 0,25 = 400 (lapsed).
Seetõttu on 25% 1600-st 400.
Selle ülesande selgeks mõistmiseks on kasulik meenutada, et iga saja elanikkonna kohta on 25 kooliealist last. Seetõttu saate kõigi kooliealiste laste arvu leidmiseks esmalt välja selgitada, mitu sadu on arvus 1600 (16), ja seejärel korrutada 25 sadade arvuga (25 x 16 = 400). Nii saate kontrollida lahenduse kehtivust.
2. ülesanne. Hoiupangad annavad hoiustajatele aastas 2% tootlust. Kui palju tulu saab hoiustaja aastas, kui ta paneb kassasse: a) 200 rubla? b) 500 rubla? c) 750 rubla? d) 1000 rubla?
Kõik neli juhtumit Probleemi lahendamiseks peate arvutama 0,02 näidatud summadest, st kõik need numbrid tuleb korrutada 0,02-ga. Teeme seda:
a) 200 0,02 = 4 (rub.),
b) 500 0,02 = 10 (rub.),
c) 750 0,02 = 15 (rub.),
d) 1000 0,02 = 20 (rub.).
Kõiki neid juhtumeid saab kontrollida järgmiste kaalutlustega. Hoiupangad annavad investoritele 2% tulu, s.o 0,02 hoiustesse hoiustatud summast. Kui summa oleks 100 rubla, siis 0,02 sellest oleks 2 rubla. See tähendab, et iga sada toob investorile 2 rubla. tulu. Seetõttu piisab igal vaadeldaval juhul sellest, kui välja mõelda, mitu sadu antud arvus on, ja korrutada 2 rubla selle arvuga sadadega. Näites a) on 2 sadu, mis tähendab
2 2 = 4 (hõõru).
Näites d) on 10 sadu, mis tähendab
2 10 = 20 (hõõru).
2. Arvu leidmine selle protsendi järgi.
Ülesanne 1. Kevadel lõpetas koolis 54 õpilast, mis moodustab 6% kooli õpilastest. Kui palju õpilasi eelmisel aastal koolis oli? õppeaasta?
Teeme kõigepealt selgeks selle ülesande tähenduse. Kooli lõpetas 54 õpilast, mis moodustab 6% õpilaste üldarvust ehk teisisõnu 6 sajandikku (0,06) kõigist kooli õpilastest. See tähendab, et teame õpilaste osa, mis on väljendatud arvuga (54) ja murdosaga (0,06) ning sellest murdosast peame leidma täisarvu. Seega on meie ees tavaline ülesanne leida arv selle murdosa hulgast (§90, lõige 6). Seda tüüpi probleemid lahendatakse jagamise teel:
See tähendab, et koolis oli ainult 900 õpilast.
Selliseid ülesandeid on kasulik kontrollida pöördülesande lahendamisega, s.t pärast ülesande lahendamist tuleks vähemalt oma peas lahendada esimest tüüpi ülesanne (antud arvu protsendi leidmine): võtke leitud arv ( 900) antud kujul ja leidke lahendatud ülesandes näidatud protsent sellest, nimelt:
900 0,06 = 54.
2. ülesanne. Perekond kulutab kuu jooksul toidule 780 rubla, mis on 65%. igakuine töötasu isa. Määrake tema igakuine sissetulek.
Sellel ülesandel on sama tähendus kui eelmisel. See annab osa igakuisest töötasust, väljendatuna rublades (780 rubla), ja näitab, et see osa moodustab 65% ehk 0,65 kogupalgast. Ja see, mida te otsite, on kogu tulu:
780: 0,65 = 1 200.
Seetõttu on nõutav sissetulek 1200 rubla.
3. Arvude protsendi leidmine.
Ülesanne 1. IN kooli raamatukogu ainult 6000 raamatut. Nende hulgas on 1200 matemaatikateemalist raamatut. Kui suur protsent matemaatikaraamatutest moodustab raamatukogus olevate raamatute koguarvu?
Oleme juba kaalunud (§97) sedalaadi probleeme ja jõudnud järeldusele, et kahe arvu protsendi arvutamiseks tuleb leida nende arvude suhe ja korrutada see 100-ga.
Meie ülesandes peame leidma arvude 1200 ja 6000 protsentuaalse suhte.
Leiame esmalt nende suhte ja seejärel korrutame selle 100-ga:
Seega on arvude 1200 ja 6000 osakaal 20. Ehk siis matemaatikaraamatud moodustavad 20% kõigi raamatute koguarvust.
Kontrollimiseks lahendame pöördülesande: leidke 20% 6000-st:
6 000 0,2 = 1 200.
2. ülesanne. Tehas peaks saama 200 tonni kivisütt. 80 tonni on juba tarnitud Mitu protsenti kivisütt on tehasesse tarnitud?
See ülesanne küsib, mitu protsenti on üks arv (80) teisest (200). Nende arvude suhe on 80/200. Korrutame selle 100-ga:
See tähendab, et 40% kivisöest on tarnitud.